样本的合理大小

一. 前言

(图: 知乎-相关问题)(题目写错了?, mmape?)

假如检索相关问题, 可以看到各种五花八门的答案, 众说纷纭.

和机器学习中的各种超参数设置一样, 统计学也有不少类似的参数悬案.

最为经典莫过于中心极限定理中要求的样本数量大于30(或者28, 29), 但是为什么是30, 却找不到相关靠谱的说明或者是数学证明, 30 这个临界值起到些什么具体的作用.

在wikipedia关于中心极限定理的介绍种也没有收录样本要求超过30类似信息.

在stackexchange有这样一个答案, 提到了关于中心极限定理中关于30的由来

[O]ne of my fellow doctoral candidates undertook a dissertation [with] a sample of only 20 cases per group. ... [L]ater I discovered ... that for a two-independent-group-mean comparison with n=30n=30 per group at the sanctified two-tailed .05.05 level, the probability that a medium-sized effect would be labeled as significant by ... a t test was only .47.47. Thus, it was approximately a coin flip whether one would get a significant result, even though, in reality, the effect size was meaningful. ... [My friend] ended up with nonsignificant results–with which he proceeded to demolish an important branch of psychoanalytic theory.

What references should be cited to support using 30 as a large enough sample size?

再看看大厂如何看待这个问题, 这是腾讯技术发的一篇相关的文章.

(图: 知乎-腾讯技术)

• zhihu_为什么 30 个样本就称为「大样本」, 而不是 40 或 50?

二. 样本大小的影响

在讨论样本合理性之前, 先探讨样本大小对于结果的影响在那些地方.

对于小样本, 毫无疑问, 不需要任何的数学证明也可知道, 样本偏小, 通常情况下显然是不利于数据的分析和相关结论得出的.

当然这里并非是指小样本都会出现这个问题, 而是说这是最直观感觉(就如同在某些期刊种的实验不可在其他实验室复现, 只是期刊作者的若干次实验的成功).

显然初步的结论是样本应该足够"大"(合适的范围起点), 才能保证结果的可靠性, 这一点应该可以肯定的.

大样本的好处, 最为直观的实验就是抛硬币, 当抛的次数足够多的情况下, 出现正反面出现的次数占比都将趋近于50%(在这里, 显然样本越大越能反映事物真实的规律).

中心极限定理

中心极限定理 是指概率论中讨论随机变量序列部分和分布渐近于正态分布的一类定理. 这组定理是数理统计学和误差分析的理论基础 指出了大量随机变量近似服从正态分布的条件. 它是概率论中最重要的一类定理 有广泛的实际应用背景. 在自然界与生产中 一些现象受到许多相互独立的随机因素的影响 如果每个因素所产生的影响都很微小时 总的影响可以看作是服从正态分布的. 中心极限定理就是从数学上证明了这一现象. 最早的中心极限定理是讨论重点 伯努利试验中 事件A出现的次数渐近于正态分布的问题.

百度百科

大数定理

大数定律好一点?

大数定理简单来说 指得是某个随机事件在单次试验中可能发生也可能不发生 但在大量重复实验中往往呈现出明显的规律性 即该随机事件发生的频率会向某个常数值收敛 该常数值即为该事件发生的概率.

知乎

上述的两个定理, 是数据处理中极为重要的两个支点(甚至于滥用).

In probability theory, the central limit theorem (CLT) establishes that, in many situations, for identically distributed independent samples, the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.

• zhihu_大数定律和中心极限定理在各个领域的运用有什么 ?
• 简明易懂的大样本理论( asymptotic/large sample theory) 的教材? - 知乎 (zhihu.com)

(图: 统计世界, 第八版, 关于推断的滥用, 抛硬币的不同次数对于显著性P值得影响)

上面的示例, 可以用更简单的t检验中t值得计算为例子

$t = \frac{\bar{x} - \mu}{s/\sqrt{n}}$

在不考虑其他得变量(或者认为其他变量的变化对于t值的影响没那么大)样本数 n 越大, t 值显然趋向于变大, 而 t 值通常用于作证显著性 P 值得可靠性.

所以换句话说 样本量越大 你越不需要靠「运气」做出「好」的结果. 而他的原话指的是第I类错误 我们上面说了 第I类错误的发生概率是我们已经通过显著性水平 ( 5%) 控制了的 所以他说的现象并不会发生. 所以呢 在我看来 至少现在我还没想到什么原因使得「大样本 」劣于「小样本」 至少从统计理论方面来看.

zhihu

三. 合理大小计算

Fisher's Exact Test

Fisher's exact test is more accurate than the chi-square test or G–test of independence when the expected numbers are small. I recommend you use Fisher's exact test when the total sample size is less than 1000, and use the chi-square or G–test for larger sample sizes. See the web page on small sample sizes for further discussion of what it means to be "small".

3.1 简单方式

(图: 统计世界, 第八版)

$e = \frac{1}{\sqrt{n}}$

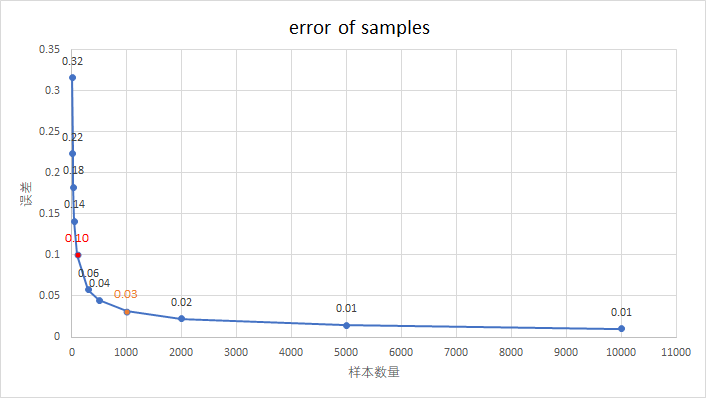
基于此, 可以绘制出样本大小-误差图.

腾讯技术文章中的1000数字来源可以通过图大致确定, 有点类似于k-means中的肘子确定 k 值法. 在1000左右, 样本数量的增加对于误差的降低的边际收益将趋于平缓.

3.2 基于z分布

有多种计算方式, 基于z分布.

$相对简单的方式:\\ n = (\frac{Z_{\sigma/2}\sigma}{E})^ 2\tag{f-1}\\$

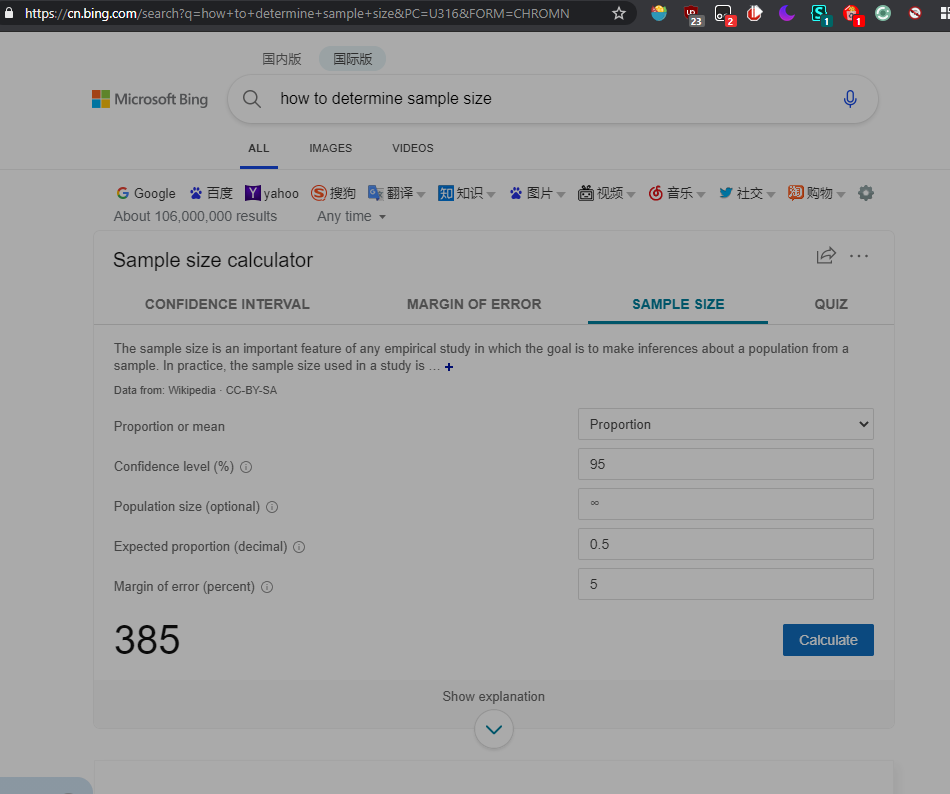
(图: bing直接提供相关计算工具, 使用的是下面的公式)

$Cochran’s Formula:\\ \\ sample = \frac{z_{score}^ 2 * StdDev * (1 - StdDev)}{margin\;of\;error} \tag{f-2}\\ z_{score}, 上图查表, \\ \alpha = 0.05(95\%)时, 两侧为0.025, 查表, 即1.96\\ StdDev = 0.5, 经验数值\\ margin\;of\;error = 0.03(根据需要自由调整)\\ 代入计算: 1067.111111$

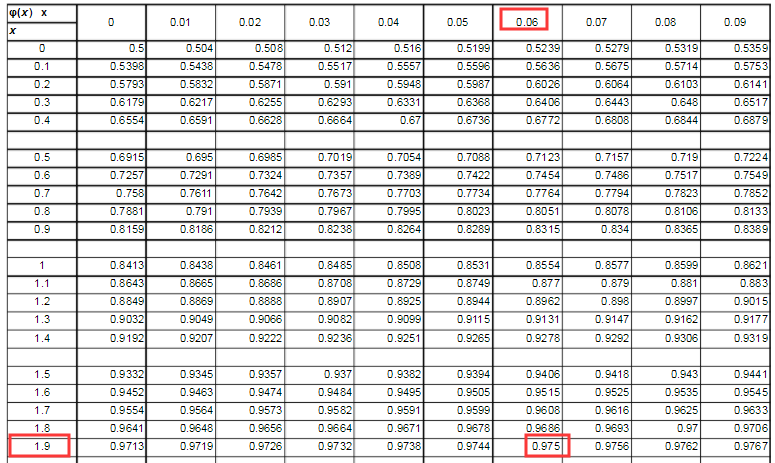
显然上述是假设总体足够大, 假如总体的数值相对较小时:

$对上述的计算进行调整:\\ n = \frac{n_0}{ 1+ \frac{(n_0 - 1)}{N}}\tag{f-3}\\ n_0, 为上述f2计算的理想数值\\ N为整体的样本数量$

示例:

A marketing research firm wants to estimate the average amount a student spends during the Spring break. They want to determine it to within $120 with 90% confidence. One can roughly say that it ranges from $100 to $1700. How many students should they sample?

$基于f1的计算方式: n = (\frac{1.645(400)}{120}) ^ 2 = 30.07\\ 400 = \frac{1700 - 100}{4}\\ 这个是对标准差的粗略估计: E = \frac{max - min}{4}\\ 或基于t检验:\\ n = (\frac{t_{\alpha/2}s}{E}) ^ 2\\ 见下面参考链接$

• 如何确定抽样统计的最小样本量( 附: 随机抽样统计的抽样误差Excel计算表格)
• z-score
• Sample Size in Statistics (How to Find it): Excel, Cochran’s Formula, General Tips

3.3 其他计算方式

Calculating Sample Size

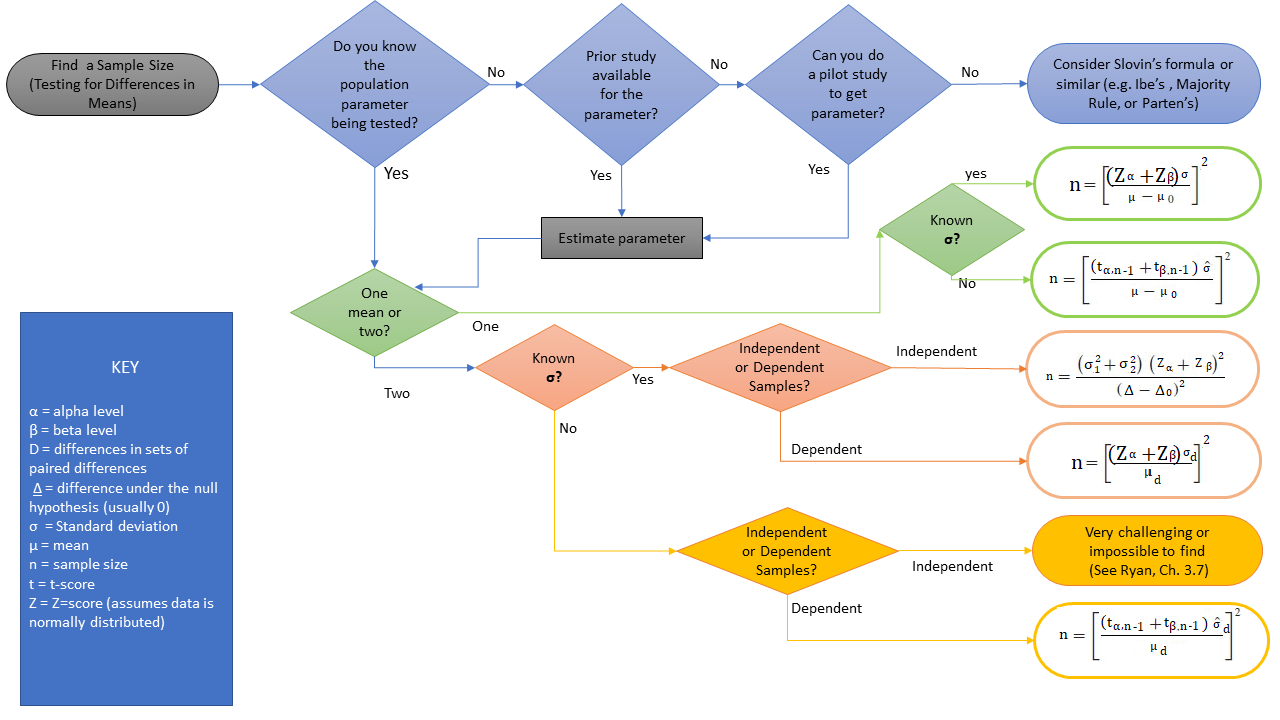
Determining Sample Size in One Picture

四. 小结

在"大数据"横行的当下, 貌似讨论样本大小没什么意义, 大规模的数据采集, 存储, 处理等等早期数理统计会遇到的问题在当下已经不再是问题, 数据当然是以大为王, 机器学习种大模型的巨大成功也在印证这种思路. 对于传统的统计方式的学习也会发现这种现象, 统计学种的一些繁琐的工作步骤, 在机器学习上是见不到的, 机器学习有时显得很粗暴, 简单, 上数据, 调优模型....当然这种简单也不是单纯靠算力来实现的, 很多还是建立在统计学/数学之上的, 只是在处理方式上, 相比于传统的数理统计发生了很大的变化.

但是, 对于诸如医学, 高精度实验等的结果验证, 这些实验多花费巨大, 或者受限的现实条件的限制, 如医学的临床测试, 显然其数据规模不可能太大, 对于样本大小的要求是必然的.

但是也应该看到传统数理统计的局限性, 和其受到计算机科学的强烈冲击的现状.

其实许多高分期刊已经开始慢慢进行不彻底的改革, 在文章中不再提"认为P＜0.05具有统计显著性", 不再报告P值水平, 而使用点估计和区间估计来替代, 或是用贝叶斯因子来替代.

"接受不确定性. 保持思考, 开放和谦逊".

事皆有多面性, 不可一叶落而天下秋.

"实际中只有凭借经验才能确定显著性检验在频率意义上的结果是否显著. 总之, 我们得到的结论, 既依赖于对类似事物的直接经验, 也依赖于我们对观测效应如何产生的一般性理解. 潜在假定的引入, 只会掩盖这一事实: 真实知识的产生过程其实是试探性的. "

Fisher

五. 参考

• < 统计世界 > 第八版
• Sample size determination with a pilot study
• 什么是统计学意义下的显著性? 如何看待统计显著性应该被淘汰了的观点?
• 神经网络为什么可以(理论上)拟合任何函数?
• Determining sample size: how to make sure you get the correct sample size
• https://www.stat.purdue.edu/~minzhang/514-Fall2021/lec%20notes_files/Lec5-samplesize.pdf