Lian
文章目录 站点概览

Lian

make thing better and simpler.

95 文章
64 标签

线性回归 - 异常

发布于 2023-05-23 | 标签: spss 、 math | 21分钟 | 4295字数

一. 前言

在一元线性回归详解 | Lian (kyouichirou.github.io), 在学生化残差章节中, 部分提及了关于帽子矩阵的内容, 这里对该部分的内容进行扩充.

该部分内容可认为是作为残差的辅助判断, 或者补充.

SPSS中关于回归-异常的计算:

相关的计算被放置在保存这个选项下(为什么会/要放在这个选项之下呢?)

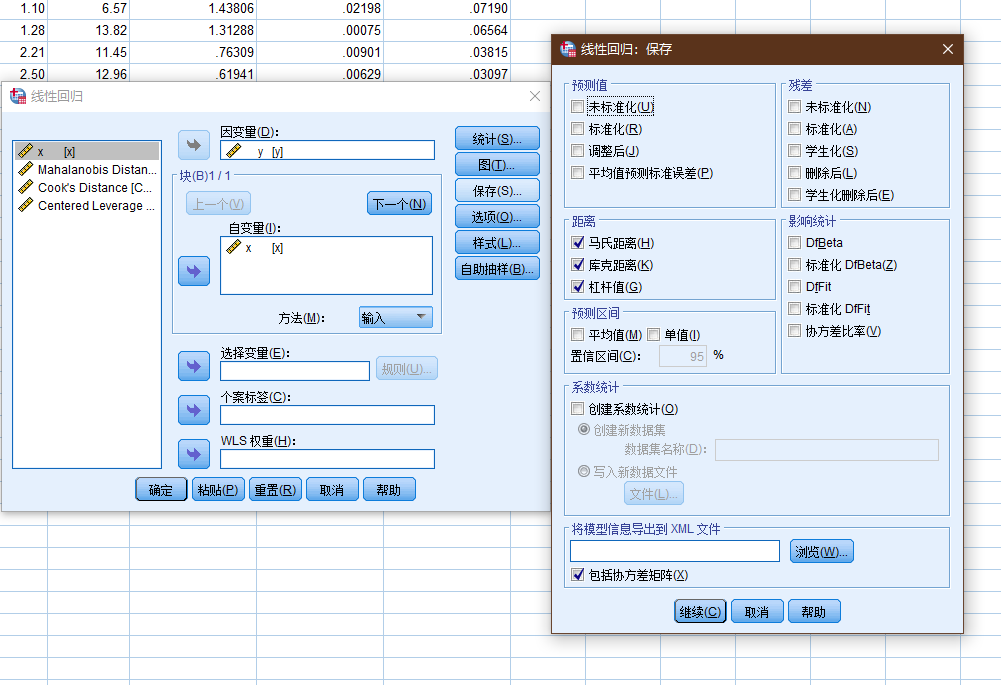
p9Tnj6H.png

距离, 标识以下个案的测量: 自变量的值具有异常组合的个案 以及可能对回归模型产生很大影响的个案.

  • Mahalanobis. 自变量上个案的值与所有个案的平均值相异程度的测量. 大的马氏距离表示个案在一个或多个自变量上具有极值.
  • Cook. 在特定个案从回归系数的计算中排除的情况下 所有个案的残差变化幅度的测量. 较大的 Cook 距离表明从回归统计的计算中排除个案之后 系数会发生根本变化.
  • 杠杆值. 度量某个点对回归拟合的影响. 集中的杠杆值范围为从 0( 对拟合无影响) 到 (N-1)/N.

Linear Regression: Saving New Variables - IBM Documentation

注意spss其中的部分计算结果和相关公式/python的计算有一定出入.

二. 异常

Row	x	    y
1	0.1	   -0.0716
2	0.45401	4.1673
3	1.09765	6.5703
4	1.27936	13.815
5	2.20611	11.4501
6	2.50064	12.9554
7	3.0403	20.1575
8	3.23583	17.5633
9	4.45308	26.0317
10	4.1699	22.7573
11	5.28474	26.303
12	5.59238	30.6885
13	5.92091	33.9402
14	6.66066	30.9228
15	6.79953	34.11
16	7.97943	44.4536
17	8.41536	46.5022
18	8.71607	50.0568
19	8.70156	46.5475
20	9.16463	45.7762

通过修改上述数据的某个值, 来演示以下的异常点对于模型的影响.

2.1 异常点

Outlier, 即观测值\hat{y}和因变量y之间残差很大的点, 即y的异常值.

Row	x	    y
1	0.1	    -0.0716
2	0.45401	4.1673
3	1.09765	6.5703
4	1.27936	13.815
5	2.20611	11.4501
6	2.50064	12.9554
7	3.0403	20.1575
8	3.23583	17.5633
9	4.45308	26.0317
10	4.1699	22.7573
11	5.28474	26.303
12	5.59238	30.6885
13	5.92091	33.9402
14	6.66066	30.9228
15	6.79953	34.11
16	7.97943	44.4536
17	8.41536	46.5022
18	8.71607	50.0568
19	8.70156	46.5475
20	9.16463	45.7762
21	4	    40
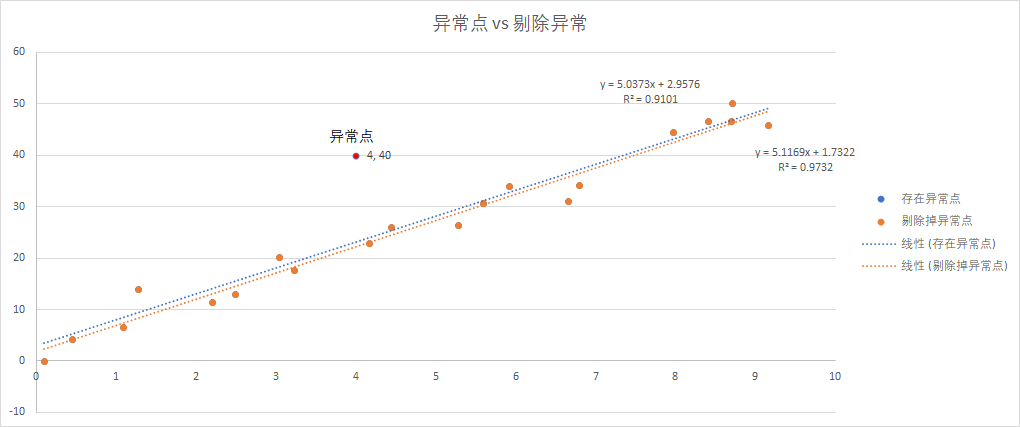
p9TSt0J.png

存在异常点和剔除掉之后的拟合方程的变化.

存在异常点:

Multiple R 0.953966
R Square 0.910051
Adjusted R Square 0.905317
标准误差 4.71075
观测值 21
df SS MS F Significance F
回归分析 1 4265.823 4265.823 192.2307 2.18E-11
残差 19 421.6322 22.19117
总计 20 4687.456
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 2.957638 2.009065 1.472147 0.157353 -1.24738 7.162659 -1.24738 7.162659
X Variable 1 5.037345 0.363321 13.86473 2.18E-11 4.276905 5.797784 4.276905 5.797784

剔除掉异常点:

Multiple R 0.986493
R Square 0.973168
Adjusted R Square 0.971677
标准误差 2.591988
观测值 20
df SS MS F Significance F
回归分析 1 4386.068 4386.068 652.8441 1.35E-15
残差 18 120.9312 6.7184
总计 19 4506.999
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 1.732178 1.120518 1.545873 0.139536 -0.62194 4.086298 -0.62194 4.086298
X Variable 1 5.116869 0.200262 25.55081 1.35E-15 4.696133 5.537605 4.696133 5.537605
COO_1 LEV_1
0.07308 0.12868
0.0058 0.10983
0.01379 0.0794
0.06749 0.07169
0.01596 0.03853
0.01391 0.03012
0.00595 0.01741
0.0045 0.01366
0.00049 0.00053
0.0018 0.00201
0.01319 0.00169
0.00025 0.00421
0.00189 0.00814
0.05628 0.02169
0.01826 0.02496
0.00527 0.062
0.00502 0.07987
0.04396 0.09352
0.00025 0.09283
0.05897 0.11587
0.36391 0.00336

二者的表现特征:

  • 异常点, 在图像上表现游离于拟合直线之外明显.
  • 剔除该点前后的标准误差变化较大, 提出后标准误差缩小, R值改善.

2.2 高杠杆点

High Leverage Point, 远离样本空间中心的点, 即自变量x的异常观测值.

高杠杆值的观测点可通过帽子统计量( hat statistic) 判断. 对于一个给定的数据集 帽子均值为 p / n 其中p是模型估计的参数数目( 包含截距项) n 是样本量. 一般来说 若观测点的帽子值大于帽子均值的2或3倍 就可以认定为高杠杆值点.

p: 即为自变量 + 1

< R语言实战 >, 第二版

Row	x	   y
1	0.1	   -0.0716
2	0.45401	4.1673
3	1.09765	6.5703
4	1.27936	13.815
5	2.20611	11.4501
6	2.50064	12.9554
7	3.0403	20.1575
8	3.23583	17.5633
9	4.45308	26.0317
10	4.1699	22.7573
11	5.28474	26.303
12	5.59238	30.6885
13	5.92091	33.9402
14	6.66066	30.9228
15	6.79953	34.11
16	7.97943	44.4536
17	8.41536	46.5022
18	8.71607	50.0568
19	8.70156	46.5475
20	9.16463	45.7762
21	14	    68
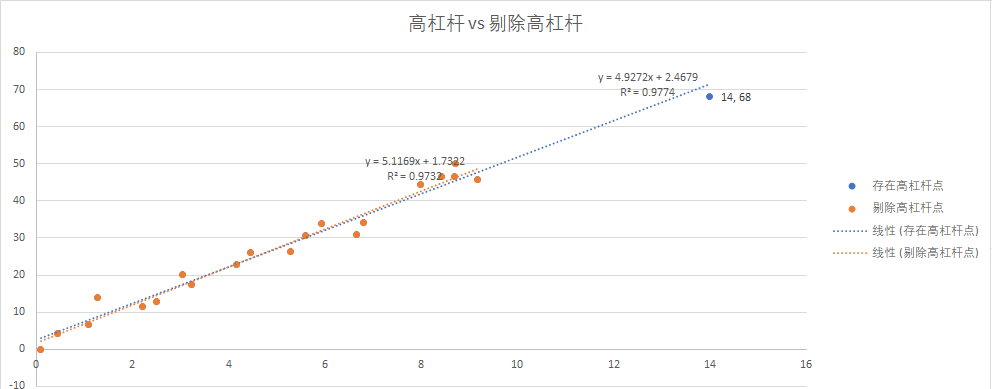
p9TpA41.png

高杠杆点:

Multiple R 0.988632
R Square 0.977393
Adjusted R Square 0.976203
标准误差 2.709112
观测值 21
df SS MS F Significance F
回归分析 1 6028.817 6028.817 821.4443 4.23E-17
残差 19 139.4465 7.339288
总计 20 6168.263
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 2.467879 1.07566 2.294293 0.03334 0.216497 4.719261 0.216497 4.719261
X Variable 1 4.927221 0.171915 28.66085 4.23E-17 4.567399 5.287043 4.567399 5.287043

剔除后:

Multiple R 0.986493
R Square 0.973168
Adjusted R Square 0.971677
标准误差 2.591988
观测值 20
df SS MS F Significance F
回归分析 1 4386.068 4386.068 652.8441 1.35E-15
残差 18 120.9312 6.7184
总计 19 4506.999
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 1.732178 1.120518 1.545873 0.139536 -0.62194 4.086298 -0.62194 4.086298
X Variable 1 5.116869 0.200262 25.55081 1.35E-15 4.696133 5.537605 4.696133 5.537605

杠杆值和cook距离

COO_1 LEV_1
0.13416 0.10586
0.0037 0.09175
0.0173 0.06867
0.24169 0.06276
0.02443 0.03675
0.02088 0.02994
0.03841 0.01926
0.00355 0.01597
0.00994 0.00241
0.00026 0.0045
0.01738 0.00001
0.0016 0.00054
0.01975 0.00194
0.08134 0.00827
0.01529 0.00995
0.04462 0.0305
0.04796 0.04093
0.1739 0.04902
0.01166 0.04861
0.03232 0.06243
0.70196 0.30992

从上述的内容来看, 剔除前后的数据, 整体的变化不大, 几个关键指标, R方, 标准误差, F值, P值等均未发生大的变化.

2.2.1 SPSS杠杆率计算

spss这里挖了个坑, 其官方文档中也没有提及为什么进行这个操作.

spss的文档不给出相关内容的计算公式, 这一点相当恶心.

使用之前文章一元线性回归详解 | Lian (kyouichirou.github.io)的数据集.

import numpy as np

# 使用之前的例子

y =np.array([
    3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
    11, 13, 13, 16, 17, 18, 17, 19, 21
])

y = y[:, np.newaxis]

x = np.array([[e, 1] for e in range(1, 21)])

xm = np.mat(x)

# 将对角线元素取出, 即为观测值的帽子量, 即杠杆率
np.diagonal((xm * (xm.T* xm).I * xm.T))

array([0.18571429, 0.15864662, 0.13458647, 0.11353383, 0.09548872,
       0.08045113, 0.06842105, 0.0593985 , 0.05338346, 0.05037594,
       0.05037594, 0.05338346, 0.0593985 , 0.06842105, 0.08045113,
       0.09548872, 0.11353383, 0.13458647, 0.15864662, 0.18571429])
COO_1 LEV_1
0.14238 0.13571
0.1185 0.10865
0.09875 0.08459
0.0117 0.06353
0.29304 0.04549
0.11503 0.03045
0.00163 0.01842
0.00113 0.0094
0.04067 0.00338
0.06076 0.00038
0.00823 0.00038
0.01761 0.00338
0.00023 0.0094
0.02095 0.01842
0.01845 0.03045
0.02411 0.04549
0.03174 0.06353
0.03783 0.08459
0.00015 0.10865
0.07319 0.13571

可以很明显的看出, spss计算的杠杆率的数值比帽子矩阵对角线元素略小, 假如拖拽相减, 会发现这个差值大概为0.05.

杠杆率的计算公式:hi=1n+(xi−xˉ)2∑i=1n(xi−xˉ)2n,为样本数量假如n趋向于无穷大,那么任意的hi≈0注:由于计算中的大量浮点数的偏差和省略,计算的结果和帽子矩阵计算有一定的差异.杠杆率的计算公式:\\ h_i = \frac{1}{n} + \frac{(x_i - \bar{x}) ^ 2}{\sum_{i=1}^n (x_i - \bar{x}) ^ 2}\\ n, 为样本数量\\ 假如n趋向于无穷大, 那么任意的h_i \approx 0\\ 注: 由于计算中的大量浮点数的偏差和省略, 计算的结果和帽子矩阵计算有一定的差异.

从上面的公式可以很快猜出该差值0.05, 就是1/n, 这个部分被spss省略.

2.2.2 帽子矩阵

hat matrix, 帽子矩阵

hat statistic, 帽子统计量

Y^=hi1Y1+hi2Y2+...+hinYn=∑j=1nhijYjy^=Xb=X(XTX)−1XTy=Hy即,H=X(XTX)−1XT\hat{Y} = h_{i1}Y_1 + h_{i2}Y_2 + ... + h_{in}Y_n = \sum_{j=1}^n h_{ij}Y_j\\ \\ \hat{y} = Xb = X(X^TX)^{-1}X^Ty = Hy\\ 即, H = X(X^TX)^{-1}X^T 

import numpy as np
from statsmodels.tools.tools import add_constant

a = np.array(
    [
    0.1,
    0.45401,
    1.09765,
    1.27936,
    2.20611,
    2.50064,
    3.0403,
    3.23583,
    4.45308,
    4.1699,
    5.28474,
    5.59238,
    5.92091,
    6.66066,
    6.79953,
    7.97943,
    8.41536,
    8.71607,
    8.70156,
    9.16463,
    14
]
)

a = a[:, np.newaxis]

a = add_constant(a)

xm = np.mat(a)

# 将对角线元素取出, 即为观测值的帽子量
np.diagonal((xm * (xm.T* xm).I * xm.T))

array([0.15348107, 0.13936727, 0.1162922 , 0.11038166, 0.0843737 ,
       0.07755662, 0.06687867, 0.06358871, 0.0500325 , 0.05212105,
       0.04763236, 0.04815593, 0.04955668, 0.05589305, 0.05757389,
       0.07812097, 0.08854887, 0.09663419, 0.09622734, 0.11004824,
       0.35753503])

h = np.diagonal((xm * (xm.T* xm).I * xm.T))

h[h > (2 * 2 / 20)]

array([0.35753503])

2.3 强影响点

Influential Point, 对模型有较大影响的点 如果删除该点能改变拟合回归方程.

强影响点 即对模型参数估计值影响有些比例失衡的点. 例如 若移除模型的一个观测点时模型会发生巨大的改变 那么你就需要检测一下数据中是否存在强影响点了. 有两种方法可以检测强影响点: Cook距离 或称D统计量 以及变量添加图( added variableplot) . 一般来说 Cook’s D值大于4/(n–k–1) 则表明它是强影响点 其中n为样本量大小 k是预测变量数目.

< R语言实战>, 第二版

Row	x	    y
1	0.1	    -0.0716
2	0.45401	4.1673
3	1.09765	6.5703
4	1.27936	13.815
5	2.20611	11.4501
6	2.50064	12.9554
7	3.0403	20.1575
8	3.23583	17.5633
9	4.45308	26.0317
10	4.1699	22.7573
11	5.28474	26.303
12	5.59238	30.6885
13	5.92091	33.9402
14	6.66066	30.9228
15	6.79953	34.11
16	7.97943	44.4536
17	8.41536	46.5022
18	8.71607	50.0568
19	8.70156	46.5475
20	9.16463	45.7762
21	13	    15
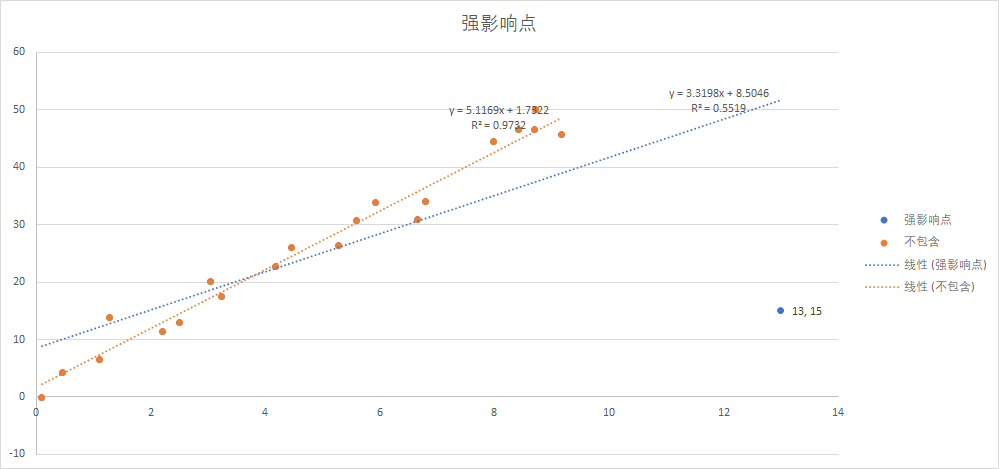
p9T1jc8.png

未剔除:

Multiple R 0.742932
R Square 0.551948
Adjusted R Square 0.528366
标准误差 10.44593
观测值 21
df SS MS F Significance F
回归分析 1 2553.978 2553.978 23.40576 0.000114
残差 19 2073.233 109.1175
总计 20 4627.211
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 8.50455 4.222417 2.014143 0.058374 -0.33307 17.34217 -0.33307 17.34217
X Variable 1 3.319798 0.686199 4.83795 0.000114 1.883566 4.756029 1.883566 4.756029

剔除后:

Multiple R 0.986493
R Square 0.973168
Adjusted R Square 0.971677
标准误差 2.591988
观测值 20
df SS MS F Significance F
回归分析 1 4386.068 4386.068 652.8441 1.35E-15
残差 18 120.9312 6.7184
总计 19 4506.999
Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 1.732178 1.120518 1.545873 0.139536 -0.62194 4.086298 -0.62194 4.086298
X Variable 1 5.116869 0.200262 25.55081 1.35E-15 4.696133 5.537605 4.696133 5.537605
COO_1 LEV_1
0.08172 0.11134
0.03076 0.09637
0.02198 0.0719
0.00075 0.06564
0.00901 0.03815
0.00629 0.03097
0.00086 0.01975
0.00095 0.0163
0.00191 0.00228
0.00004 0.0044
0.00002 0.00005
0.0032 0.00074
0.00848 0.00237
0.00003 0.00947
0.0028 0.01132
0.03958 0.03383
0.05229 0.04518
0.0918 0.05397
0.04809 0.05353
0.03194 0.06853
4.04801 0.26391

从上面的内容看, 删除异常点前后, 所有关键指标均发生变化, 基本等同于两个不同的模型.

2.3.1 cook距离计算

Di=(yi−yi^)2(m+1)s2hi(1−hi)2m,为自变量的数量,一元线性,m=1...如此D_i= \frac{(y_i - \hat{y_i}) ^ 2}{(m + 1)s^2}\frac{h_i}{(1 - h_i)^2}\\ m, 为自变量的数量, 一元线性, m = 1...如此

有趣的是这里的计算, spss使用的帽子矩阵方式计算的杠杆值, 而不是它自己给出的杠杆值, 实在无厘头.

y_e COO_1 LEV_1 hand_cook new_lev
-8.90813 0.08172 0.11134 0.081715 0.158959
-5.84447 0.03076 0.09637 0.030756 0.143989
-5.57823 0.02198 0.0719 0.021982 0.119519
1.063233 0.00075 0.06564 0.000746 0.113259
-4.37829 0.00901 0.03815 0.009014 0.085769
-3.85077 0.00629 0.03097 0.00629 0.078589
1.559769 0.00086 0.01975 0.000863 0.067369
-1.68355 0.00095 0.0163 0.000947 0.063919
2.743825 0.00191 0.00228 0.001907 0.049899
0.409525 0.00004 0.0044 4.45E-05 0.052019
0.254181 0.00002 0.00005 1.56E-05 0.047669
3.618379 0.0032 0.00074 0.003204 0.048359
5.779426 0.00848 0.00237 0.008477 0.049989
0.306205 0.00003 0.00947 2.76E-05 0.057089
3.032385 0.0028 0.01132 0.002804 0.058939
9.458956 0.03958 0.03383 0.039577 0.081449
10.06036 0.05229 0.04518 0.052292 0.092799
12.61666 0.0918 0.05397 0.091804 0.101589
9.15553 0.04809 0.05353 0.048087 0.101149
6.846931 0.03194 0.06853 0.031939 0.116149
-36.6619 4.04801 0.26391 4.047933 0.311529 
hand_cook = y_e/2/标准误差^2 * new_lev/(1- new_lev)^2

# new_lev, 恢复原来的杠杆值

通过图形可以判断Alaska Hawaii和Nevada是强影响点. 若删除这些点 将会导致回归模型截距项和斜率发生显著变化. 注意 虽然该图对搜寻强影响点很有用 但我逐渐发现以1为分割点比4/(n–k–1)更具一般性. 若设定D=1为判别标准 则数据集中没有点看起来像是强影响点.

< R语言实战 >

确定某一观察点是否具有影响的经验规则是其库克距离超过1.0. 更精确地说 也可以比较库克距离与具有( m n-m-1) 自由度的 F FF 分布的百分位数. 如果观察值位于该分布的第1个四分之一位( 低于25%) 则观察点对回归的影响较小. 如果库克距离大于该分布的中位数 则该观察点具有一定的影响.

15 离群点和高杠杆率点_库克距离_纸境止境的博客-CSDN博客

2.4 小结

  • 异常点不一定是强影响点 强影响点也不一定是异常点.
  • 高杠杆点不一定是强影响点 强影响点也不一定是高杠杆点.

2.5 异常的处理

  • 删除异常观测点.

    删除离群点通常可以提高数据集对于正态假设的拟合度 而强影响点会干扰结果 通常也会被删除. 删除最大的离群点或者强影响点后 模型需要重新拟合. 若离群点或强影响点仍然存在 重复以上过程直至获得比较满意的拟合. 我对删除观测点持谨慎态度. 若是因为数据记录错误 或是没有遵守规程 或是受试对象误解了指导说明 这种情况下的点可以判断为离群点 删除它们是十分合理的.

    不过在其他情况下 所收集数据中的异常点可能是最有趣的东西. 发掘为何该观测点不同于其他点 有助于你更深刻地理解研究的主题 或者发现其他你可能没有想过的问题. 我们一些最伟大的进步正是源自于意外地发现了那些不符合我们先验认知的东西( 抱歉 我说得夸张了) .

    简而言之, 删除异常点需谨慎, 查找异常的来源也是对数据很好的探索方式之一.

  • 变量变换, 相对常见的就是Box-Cox正态变换, 让数据更趋向于满足正态分布.

  • 添加变量或者删除变量(注意是变量, 不是观测点, 变量, 列)

  • 使用其他的回归方法

三. 参考

# spss # math
地址拆分-Excel公式执行循环操作 上一篇
2022 Kaggle Data Science & ML Survey 下一篇
已运行:
浏览数: 次 | 访客数: 人
Powered by Kyouichirou