
(上图: 号称难度系数最高数独)
数独是一个非常有趣的数学游戏, 最为常见的形式为九宫格(也有四宫格, 六宫格等): 9 x 9
- 每个格子填入
1 - 9范围的数字, 每个格子填入的数字都不相同 - 每个小宫格
3 x 3范围填入, 遵守上述规则 - 行列之间的数字填入, 遵守上述规则
数独这个问题的解法非常巧妙, 这里参考了通过整数规划求解数独谜题: 基于问题 - MATLAB & Simulink - MathWorks 中国提供的思路.
(MATLAB的文档是很不错的资料源, 对于各类数学/工程问题)
关键思路是将谜题从 9×9 正方形网格转换为一个由二元值( 0 或 1) 组成的 9×9×9 立方数组. 将这个立方数组想象成由 9 个正方形网络上下堆叠在一起. 顶部网格是数组的第一个正方形层, 只要解或提示包含整数 1, 则该层对应位置就为 1. 只要解或提示包含整数 2, 第二层对应位置就为 1. 只要解或提示包含整数 9, 第九层对应位置就为 1.
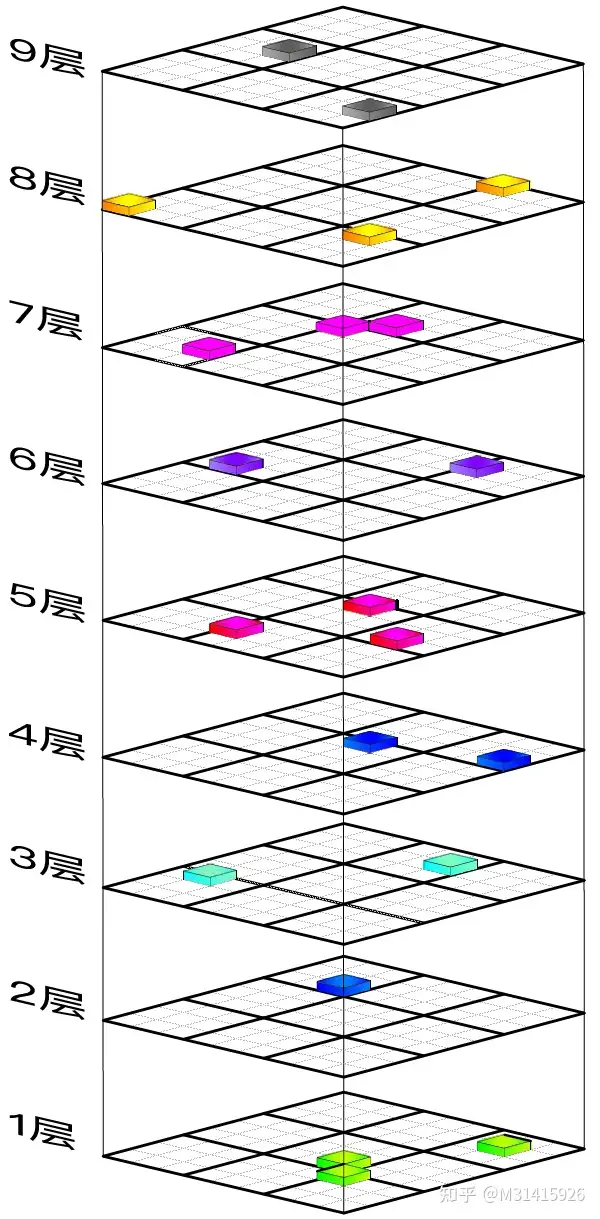
(图源: 数学建模代码实战训练-5: 数独里的整数线规模型构造分析 - 知乎, 作者版权所有)
以整数规划为视角创建数学模型:
一. 整数规划
使用 pyscipopt来求解
import pyscipopt as opt
# 创建上述数独
matrix = [
[8, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 6, 0, 0, 0, 0, 0],
[0, 7, 0, 0, 9, 0, 2, 0, 0],
[0, 5, 0, 0, 0, 7, 0, 0, 0],
[0, 0, 0, 0, 4, 5, 7, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 3, 0],
[0, 0, 1, 0, 0, 0, 0, 6, 8],
[0, 0, 8, 5, 0, 0, 0, 1, 0],
[0, 9, 0, 0, 0, 0, 4, 0, 0]
]
# 普通参数
# matrix shape
N = 9
# litte matrix shape
n = 3
# 填入的数字
constants = [e for e in range(1, N + 1)]
model = opt.Model("sudoku")
# 创建变量, 需要 9 * 9 * 9 = 729个决策变量
variables = {}
for r in range(N):
for c in range(N):
for k in constants:
key = (r, c, k)
variables[key] = model.addVar(
name = '_'.join(str(e) for e in key),
# 数据类型为布尔型, 即0, 1
vtype = 'B'
)
# 同时这里实现上述模型中的决策变量 0-1约束
# 约束1, 对已经填写了数字变量坐标添加1策略约束
for r in range(N):
for c in range(N):
if matrix[r][c] != 0:
constrain = variables[(r, c, matrix[r][c])] == 1
model.addCons(constrain)
# 约束2, 每个网格内有且只有一个数字
for r in range(N):
for c in range(N):
constrain = opt.quicksum(variables[(r, c, k)] for k in constants) == 1
model.addCons(constrain)
# 约束3, 行列约束
for i in range(N):
for k in constants:
# 行约束
r_constrain = opt.quicksum(variables[i, c, k] for c in range(N)) == 1
model.addCons(r_constrain)
# 列约束
c_constrain = opt.quicksum(variables[r, i, k] for r in range(N)) == 1
model.addCons(c_constrain)
# 约束4, 子宫格约束
for row in range(n):
for col in range(n):
for k in constants:
constrain = opt.quicksum(variables[r + n * row, c + n * col, k] for r in range(n) for c in range(n)) == 1
model.addCons(constrain)
# 无目标函数
model.optimize()
if model.getStatus() == 'optimal':
print('sudoku solution:')
# 预先构造一个数独容器用于存放解析结果
solution = [[0 for _ in range(N)] for _ in range(N)]
for (r, c, k) in variables.keys():
if model.getVal(variables[r, c, k]) == 1:
solution[r][c] = k
# 绘制数独结果
sudo_data = (''.join(f'{"| " if c % 3 == 0 else " "}{solution[r][c]}{" " if matrix[r][c] == 0 else "*"}' for c in range(N)) + '|' + ('\n'+ '-' * 31 if (r + 1) % 3 == 0 and r != N - 1 else '') for r in range(N))
print('\n'.join(sudo_data))
else: print('warning: no solution')
sudoku solution:
| 8* 1 2 | 7 5 3 | 6 4 9 |
| 9 4 3*| 6* 8 2 | 1 7 5 |
| 6 7* 5 | 4 9* 1 | 2* 8 3 |
-------------------------------
| 1 5* 4 | 2 3 7*| 8 9 6 |
| 3 6 9 | 8 4* 5*| 7* 2 1 |
| 2 8 7 | 1* 6 9 | 5 3* 4 |
-------------------------------
| 5 2 1*| 9 7 4 | 3 6* 8*|
| 4 3 8*| 5* 2 6 | 9 1* 7 |
| 7 9* 6 | 3 1 8 | 4* 5 2 |
二. 约束规划
使用ortools的规划约束来求解.
整体的解决思路还是类似的, 但是由于cp_model模型提供了更为简单的方式来实现, 所以更为简单优雅.
AddAllDifferent这个函数的理解, 即对多个可迭代变量进行约束, 每个变量完全不重复.
但是需要注意和excel提供的相类似的方法不同, AddAllDifferent对变量约束之后, 可以进行二度约束.
def AddAllDifferent(self, variables)
Adds AllDifferent(variables).
This constraint forces all variables to have different values.
Args
variables
a list of integer variables.
Returns
An instance of the Constraint class.
vba调用规划求解模块, 无法使用AddAllDifferent约束来实现数独的求解.
Sub sudoku_test()
Const N As Integer = 9, M As Integer = 3
Dim r As Integer, c As Integer, i As Integer, j As Integer
'重置求解器'
SolverReset
'设置求解器目标等 '
SolverOk MaxMinVal:=0, ValueOf:=0, ByChange:="$A$1:$I$9", Engine:=1, EngineDesc _
:="GRG Nonlinear"
' 整体约束 --------
' 整数约束
SolverAdd CellRef:="$A$1:$I$9", Relation:=4, FormulaText:="整数"
' 数字约束, 大于等于1
SolverAdd CellRef:="$A$1:$I$9", Relation:=3, FormulaText:="1"
' 数字约束, 小于等于9
SolverAdd CellRef:="$A$1:$I$9", Relation:=1, FormulaText:="9"
' ------ 整体约束
' 已经填入的数字约束, 这部分的约束和AllDifferent冲突
For r = 1 To N
For c = 1 To N
i = Cells(r, c).Value
If i > 0 Then
SolverAdd CellRef:=Range(Cells(r, c), Cells(r, c)), Relation:=2, FormulaText:=CStr(i)
End If
Next
Next
' 行约束
For r = 1 To N
SolverAdd CellRef:=Range(Cells(r, 1), Cells(r, 9)), Relation:=6, FormulaText:="AllDifferent"
Next
' 列约束
For c = 1 To N
SolverAdd CellRef:=Range(Cells(1, c), Cells(9, c)), Relation:=6, FormulaText:="AllDifferent"
Next
' 小宫格约束
i = 1
j = 1
For r = 1 To M
For c = 1 To M
SolverAdd CellRef:=Range(Cells(i, j), Cells(i + 2, j + 2)), Relation:=6, FormulaText:="AllDifferent"
j = j + 3
Next
i = i + 3
j = 1
Next
SolverSolve
End Sub
已经填入的数字约束, 这部分的约束和AllDifferent冲突.
from ortools.sat.python import cp_model
# 在求解上稍微有点不一样, model并没有solver()
model = cp_model.CpModel()
# 需要创建一个求解器的实例
solver = cp_model.CpSolver()
variables = {}
for r in range(N):
for c in range(N):
variables[r, c] = cell if (cell := matrix[r][c]) != 0 else model.NewIntVar(1, N, f'v[{r}{c}]')
for r in range(N):
model.AddAllDifferent((variables[r, c] for c in range(N)))
for c in range(N):
model.AddAllDifferent((variables[r, c] for r in range(N)))
for row in range(n):
for col in range(n):
model.AddAllDifferent((variables[r + n * row, c + n * col] for r in range(n) for c in range(n)))
status = solver.Solve(model)
if status == cp_model.OPTIMAL:
print('sudoku solution:')
# 预先构造一个数独容器用于存放解析结果
solution = [[0 for _ in range(N)] for _ in range(N)]
for i in range(N):
for j in range(N):
solution[i][j] = int(solver.Value(variables[i, j]))
# 绘制数独结果
sudo_data = (''.join(f'{"| " if c % 3 == 0 else " "}{solution[r][c]}{" " if matrix[r][c] == 0 else "*"}' for c in range(N)) + '|' + ('\n'+ '-' * 31 if (r + 1) % 3 == 0 and r != N - 1 else '') for r in range(N))
print('\n'.join(sudo_data))
else: print('warning: no solution')
sudoku solution:
| 8* 1 2 | 7 5 3 | 6 4 9 |
| 9 4 3*| 6* 8 2 | 1 7 5 |
| 6 7* 5 | 4 9* 1 | 2* 8 3 |
-------------------------------
| 1 5* 4 | 2 3 7*| 8 9 6 |
| 3 6 9 | 8 4* 5*| 7* 2 1 |
| 2 8 7 | 1* 6 9 | 5 3* 4 |
-------------------------------
| 5 2 1*| 9 7 4 | 3 6* 8*|
| 4 3 8*| 5* 2 6 | 9 1* 7 |
| 7 9* 6 | 3 1 8 | 4* 5 2 |
对于数独问题, 约束规划相对于整数规划更为容易理解.
CP has a widespread and very active community around the world with dedicated scientific journals, conferences, and an arsenal of different solving techniques . CP has been successfully applied in planning, scheduling, and numerous other domains with heterogeneous constraints.
在实际的应用中, 约束规划的求解可能有更好的适应性.
