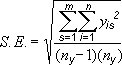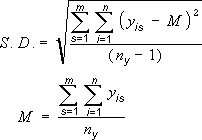关于Excel图表中误差线的计算问题

一. 问题

构造数据

This option	Uses this equation
Standard Error
Standard Deviation

Standard Error

Where:

s = series number

i = point number in series s

m = number of series for point y in chart

n = number of points in each series

yis = data value of series s and the ith point

ny = total number of data values in all series

Standard Deviation

Where:

s = series number

i = point number in series s

m = number of series for point y in chart

n = number of points in each series

yis = data value of series s and the ith point

ny = total number of data values in all series

M = arithmetic mean

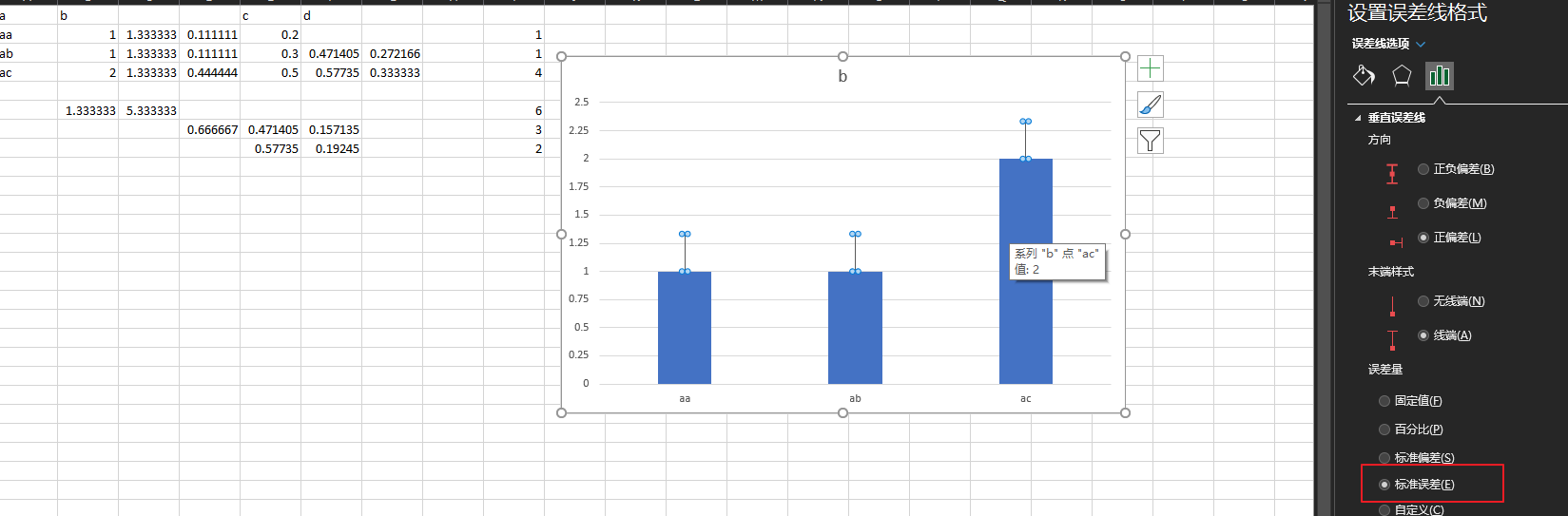
用这个上述的数据, 首先是手动计算这个标准偏差

F3=STDEV.S(B2:B4)

S. E =F3/SQRT(3)

注意, 这里使用的计算标准偏差使用的时STDEV.S不是STDEV.P(经过测试, S得到的数据结果是和excel绘制的标准误差线是一致的).

二者的差异

• STDEV.S

  基于样本估算标准偏差

  $S.D_s = \sqrt{\frac{\sum(x - \bar x)^ 2}{(n- 1)}}$

• STDEV.P

  计算基于以参数形式给出的整个样本总体的标准偏差

  $S.D_p = \sqrt{\frac{\sum(x - \bar x)^ 2}{n}}$

标准误差(standard error)的计算

$S.E = \frac{S.D}{\sqrt{n}}$

其中

• S.D为标准偏差(standard deviation),
• n为样本的数量

按照上述的计算方式, 来执行, 和excel绘制的误差线完全契合.

但是微软给出的文档中的内容, 标准偏差的计算没什么疑问, 但是这个标准误差这里的计算方式(或者说写法)就有那么一点问题.

$S.E = \sqrt{\frac{\sum_{s=1}^{m}\sum_{i=1}^{n}y^2_{is}}{(n_y -1)(n_y)}}$

yis = data value of series s and the ith point

但是计算流程

$S.D = \sqrt{\frac{\sum_{s=1}^{m}\sum_{i=1}^{n}(y_{is} - M) ^ 2}{(n_y-1)}}$

$S.E = \frac{S.D}{\sqrt{n_y}}$

$S.E = \sqrt{\frac{\sum_{s=1}^{m}\sum_{i=1}^{n}(y_{is} - M) ^ 2}{(n_y-1)(n_y)}}$

不清楚微软这么写的方式, 也许微软写这个的时候认为:

$y_{is} = y_{is} - M$

二. 其他

Standard deviation: Quantifies the variability of values in a dataset. It assesses how far a data point likely falls from the mean.
Standard error: Quantifies the variability between samples drawn from the same population. It assesses how far a sample statistic likely falls from a population parameter.

首先 从英文名字来讲 标准偏差是standard deviation deviation有"离差"的意思. 标准偏差表征的是数据的离散程度; 而标准误差的英文名是standard error 表征的是单个统计量在多次抽样中呈现出的变异性. 可以这样理解 前者是表示数据本身的变异性 而后者表征的是抽样行为的变异性.

• Difference Between Standard Deviation and Standard Error - Statistics By Jim
• 标准差 标准误 标准误差 ? ? ? - 知乎 (zhihu.com)

注: 大量的统计术语由于汉语翻译时语境(语义)相近, 导致很多内容的表述出现混乱, 尽量中英搭配出现.