一. 基本概念
1.1 矩阵
Matrix.
矩阵的本质是什么? - 知乎 (zhihu.com)
A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . . . . . . . . . . a m 1 a m 2 . . . a m n ] m = n , 则 称 为 方 阵 , 或 者 m 阶 矩 阵 ; 不 同 的 方 阵 之 间 存 在 相 同 的 行 列 数 , 则 称 为 同 阶 矩 阵 . m = 1 , 则 称 为 行 矩 阵 , 也 称 n 维 行 向 量 ; n = 1 , 则 称 为 列 矩 阵 , 也 称 m 维 列 向 量 . \mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & ... &a_{1n} \\ a_{21} & a_{22} & ... &a_{2n} \\ ... & ... & ... &... \\ a_{m1} & a_{m2} & ... &a_{mn} \end{bmatrix}\\
m = n, 则称为方阵, 或者m阶矩阵;\\
不同的方阵之间存在相同的行列数, 则称为同阶矩阵.\\
m = 1, 则称为行矩阵, 也称n维行向量;\\
n = 1, 则称为列矩阵, 也称m维列向量.
A = ⎣ ⎢ ⎢ ⎡ a 1 1 a 2 1 . . . a m 1 a 1 2 a 2 2 . . . a m 2 . . . . . . . . . . . . a 1 n a 2 n . . . a m n ⎦ ⎥ ⎥ ⎤ m = n , 则 称 为 方 阵 , 或 者 m 阶 矩 阵 ; 不 同 的 方 阵 之 间 存 在 相 同 的 行 列 数 , 则 称 为 同 阶 矩 阵 . m = 1 , 则 称 为 行 矩 阵 , 也 称 n 维 行 向 量 ; n = 1 , 则 称 为 列 矩 阵 , 也 称 m 维 列 向 量 .
1.2 秩
The Rank of Matrix
矩阵的秩是线性代数中的一个概念. 在线性代数中 一个矩阵A的列秩是A的线性独立的纵列的极大数 通常表示为r(A) rk(A)或rank A. 在线性代数中 一个矩阵A的列秩是A的线性独立的纵列的极大数目. 类似地 行秩是A的线性无关的横行的极大数目. 即如果把矩阵看成一个个行向量或者列向量 秩就是这些行向量或者列向量的秩 也就是极大无关组中所含向量的个数.
矩阵的秩_百度百科 (baidu.com)
常 见 表 示 : r a n k ( A ) , r k ( A ) , r ( A ) 秩 的 特 性 : 1. 转 置 后 秩 不 变 2. R ( A ) ≤ m i n { m , n } , A 是 m 行 n 列 矩 阵 3. R ( k A ) = R ( A ) , k ≠ 0 4. R ( A ) = 0 → A = 0. 5. R ( A + B ) ≤ R ( A ) + R ( B ) A 为 n 阶 方 阵 时 . R ( A ) = n 称 A 是 满 秩 阵 ( 非 奇 异 矩 阵 ) R ( A ) < n 称 A 是 降 秩 阵 ( 奇 异 矩 阵 ) R ( A ) = n ⟺ ∣ A ∣ ≠ 0 对 于 满 秩 方 阵 A 施 行 初 等 行 变 换 可 以 化 为 单 位 阵 E 又 根 据 初 等 阵 的 作 用 . 每 对 A 施 行 一 次 初 等 行 变 换 相 当 于 用 一 个 对 应 的 初 等 阵 左 乘 A 由 此 得 到 下 面 的 定 理 A = [ 1 2 3 2 1 2 3 1 2 ] − r 2 − 2 r 1 r 3 − 3 r 1 → [ 1 2 3 0 − 3 − 4 0 − 2 − 3 ] − r 1 + r 3 r 2 − r 3 → [ 1 0 0 0 − 1 − 1 0 − 2 − 3 ] − ( − r 3 + 2 r 2 ) → [ 1 0 0 0 − 1 − 1 0 0 1 ] − ( − r 2 − r 3 ) → [ 1 0 0 0 1 0 0 0 1 ] = E R ( A ) = 3 A 为 满 秩 方 阵 . 常见表示: rank(A), rk(A), r(A)\\
秩的特性:\\
1. 转置后秩不变\\
2. R(A) \leq min\{m, n\}, A是m行n列矩阵\\
3. R(kA) = R(A), k \neq 0\\
4. R(A) = 0 \rightarrow A = 0.\\
5. R(A + B) \leq R(A) + R(B)
\\\\
A为n阶方阵时.\\
R ( A ) = n 称A是满秩阵 (非奇异矩阵)\\
R ( A ) < n 称A是降秩阵 (奇异矩阵)\\
R(A) = n ⟺ ∣A∣ \neq 0\\
\\\\
对于满秩方阵A施行初等行变换可以化为单位阵E 又根据初等阵的作用.\\
每对A施行一次初等行变换 相当于用一个对应的初等阵左乘A 由此得到下面的定理\\
A = \begin{bmatrix} 1 & 2 & 3 \\2 & 1 & 2 \\ 3 & 1 & 2 \\ \end{bmatrix}\\
-\begin{matrix} {r_2-2r_1} \\ {r_3-3r_1} \end{matrix}\rightarrow
\begin{bmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & -2 & -3 \\ \end{bmatrix}-\begin{matrix} {r_1+r_3} \\ {r_2-r_3} \end{matrix} \rightarrow\\
\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & -1 \\ 0 & -2 & -3 \\ \end{bmatrix}\\
-\begin{matrix} {(-r_3+2r_2)} \end{matrix}\rightarrow\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & -1 \\ 0 & 0 & 1 \\ \end{bmatrix}-\begin{matrix} {(-r_2-r_3)}\end{matrix}\rightarrow\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} = E\\
R(A)=3 A为满秩方阵.
常 见 表 示 : r a n k ( A ) , r k ( A ) , r ( A ) 秩 的 特 性 : 1 . 转 置 后 秩 不 变 2 . R ( A ) ≤ m i n { m , n } , A 是 m 行 n 列 矩 阵 3 . R ( k A ) = R ( A ) , k = 0 4 . R ( A ) = 0 → A = 0 . 5 . R ( A + B ) ≤ R ( A ) + R ( B ) A 为 n 阶 方 阵 时 . R ( A ) = n 称 A 是 满 秩 阵 ( 非 奇 异 矩 阵 ) R ( A ) < n 称 A 是 降 秩 阵 ( 奇 异 矩 阵 ) R ( A ) = n ⟺ ∣ A ∣ = 0 对 于 满 秩 方 阵 A 施 行 初 等 行 变 换 可 以 化 为 单 位 阵 E 又 根 据 初 等 阵 的 作 用 . 每 对 A 施 行 一 次 初 等 行 变 换 相 当 于 用 一 个 对 应 的 初 等 阵 左 乘 A 由 此 得 到 下 面 的 定 理 A = ⎣ ⎡ 1 2 3 2 1 1 3 2 2 ⎦ ⎤ − r 2 − 2 r 1 r 3 − 3 r 1 → ⎣ ⎡ 1 0 0 2 − 3 − 2 3 − 4 − 3 ⎦ ⎤ − r 1 + r 3 r 2 − r 3 → ⎣ ⎡ 1 0 0 0 − 1 − 2 0 − 1 − 3 ⎦ ⎤ − ( − r 3 + 2 r 2 ) → ⎣ ⎡ 1 0 0 0 − 1 0 0 − 1 1 ⎦ ⎤ − ( − r 2 − r 3 ) → ⎣ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎤ = E R ( A ) = 3 A 为 满 秩 方 阵 .
a = np.mat([
[401, -201],
[-800, 401]
])
np.linalg.matrix_rank(a)
2
np.linalg.matrix_rank(np.mat([
[1, 2],
[2, 4]
]))
1
1.3 迹
Trace
一个n×n矩阵A(方阵 )的主对角线( 从左上方至右下方的对角线) 上各个元素的总和被称为矩阵A的迹( 或迹数) 一般记作tr(A).
https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E7%9A%84%E8%BF%B9?fromModule=lemma_search-box
t r ( A ) = a 11 + . . . + a n n = ∑ i = 1 n a i i . t r ( A ) = t r ( A T ) , 转 置 不 改 变 主 对 角 线 的 元 素 t r ( A + B ) = t r ( A ) + t r ( B ) t r ( A B ) = t r ( B A ) t r ( A B C ) = t r ( C B A ) = t r ( B C A ) tr ( ( A ⊙ B ) T C ) = tr ( ( A ) T ( B ⊙ C ) ) 矩 阵 乘 法 和 迹 交 换 其 中 ⊙ 是 哈 德 玛 积 即 对 应 元 素 之 积 . tr ( A ) = ∑ k = 1 n λ k , 矩 阵 的 迹 等 于 矩 阵 特 征 值 之 和 . ∴ t r ( A ) = t r ( Q Λ Q − 1 ) = t r ( Λ Q − 1 Q ) = t r ( Λ ) 若 A 是 实 对 称 矩 阵 , 则 A = t r ( Q Λ Q T ) t r ( A T A ) = t r ( Q Λ Q T Q Λ Q T ) = t r ( Q Λ 2 Q T ) = t r ( Λ 2 Q T Q ) = t r ( Λ 2 ) 矩 阵 的 二 次 型 用 迹 来 表 示 : x T A x = t r ( A x x T ) 求 导 : ∂ T r ( A B ) ∂ A = B T ∂ T r ( A B ) ∂ A = ∂ ∑ i = 1 m ∑ j = 1 n a i j b j i ∂ ∑ i = 1 m ∑ j = 1 n a i j = ∑ i = 1 m ∑ j = 1 n b j i = B T ∂ T r ( A B A T C ) ∂ A = ∂ T r ( A T C A B ) ∂ A = ∂ T r ( A C T A T B T ) ∂ A = C A B + ( B A T C ) T = C A B + C T A B T 若 不 使 用 求 和 符 号 有 些 矩 阵 运 算 很 难 描 述 而 通 过 矩 阵 乘 法 和 迹 运 算 符 号 可 以 清 楚 地 表 示 . 例 如 迹 运 算 提 供 了 另 一 种 描 述 矩 阵 F r o b e n i u s 范 数 的 方 式 : ∣ ∣ A ∣ ∣ F = T r ( A A T ) tr(A)=a_{11}+...+a_{nn}=\sum\limits_{i=1}^{n} a_{ii}.\\
tr(A) = tr(A^T), 转置不改变主对角线的元素\\
tr(A + B) = tr(A) + tr(B)\\
tr(AB) = tr(BA)\\
tr(ABC) = tr(CBA) = tr(BCA)\\
\\
\operatorname{tr}((\mathbf{A}\odot\mathbf{B})^T\mathbf{C})=\operatorname{tr}((\mathbf{A})^T(\mathbf{B}\odot\mathbf{C}))\\
矩阵乘法和迹交换 其中 ⊙ 是哈德玛积 即对应元素之积.
\\
\\
\operatorname{tr}(\mathbf{A})=\sum_{k=1}^n\lambda_k, 矩阵的迹等于矩阵特征值之和.\\
\therefore tr(A)=tr(Q\Lambda Q^{-1})=tr(\Lambda Q^{-1}Q)=tr(\Lambda)\\
若A是实对称矩阵, 则A=tr(Q\Lambda Q^{T})\\
tr(A^TA)=tr(Q\Lambda Q^{T}Q\Lambda Q^{T})=tr(Q\Lambda ^{2} Q^{T})=tr(\Lambda ^{2} Q^{T}Q)=tr(\Lambda^{2} )\\
\\
矩阵的二次型用迹来表示: x^TAx=tr(Axx^T)\\
\\
求导:\\
\frac{\partial Tr(AB)}{\partial A}=B^T\\
\frac{\partial Tr(AB)}{\partial A}=\frac{\partial \sum\limits_{i=1}^m\sum\limits_{j=1}^na_{ij}b_{ji}}{\partial\sum\limits_{i=1}^m\sum\limits_{j=1}^na_{ij}}=\sum\limits_{i=1}^m\sum\limits_{j=1}^nb_{ji}=B^T\\
\frac{\partial Tr(ABA^TC)}{\partial A}=\frac{\partial Tr(A^TCAB)}{\partial A}=\frac{\partial Tr(AC^TA^TB^T)}{\partial A}=CAB+(BA^TC)^T=CAB+C^TAB^T\\
\\
若不使用求和符号 有些矩阵运算很难描述 而通过矩阵乘法和迹运算符号可以清楚地表示. \\
例如 迹运算提供了另一种描述矩阵Frobenius范数的方式: \\
||A||_F=\sqrt{Tr(AA^T)}
t r ( A ) = a 1 1 + . . . + a n n = i = 1 ∑ n a i i . t r ( A ) = t r ( A T ) , 转 置 不 改 变 主 对 角 线 的 元 素 t r ( A + B ) = t r ( A ) + t r ( B ) t r ( A B ) = t r ( B A ) t r ( A B C ) = t r ( C B A ) = t r ( B C A ) t r ( ( A ⊙ B ) T C ) = t r ( ( A ) T ( B ⊙ C ) ) 矩 阵 乘 法 和 迹 交 换 其 中 ⊙ 是 哈 德 玛 积 即 对 应 元 素 之 积 . t r ( A ) = k = 1 ∑ n λ k , 矩 阵 的 迹 等 于 矩 阵 特 征 值 之 和 . ∴ t r ( A ) = t r ( Q Λ Q − 1 ) = t r ( Λ Q − 1 Q ) = t r ( Λ ) 若 A 是 实 对 称 矩 阵 , 则 A = t r ( Q Λ Q T ) t r ( A T A ) = t r ( Q Λ Q T Q Λ Q T ) = t r ( Q Λ 2 Q T ) = t r ( Λ 2 Q T Q ) = t r ( Λ 2 ) 矩 阵 的 二 次 型 用 迹 来 表 示 : x T A x = t r ( A x x T ) 求 导 : ∂ A ∂ T r ( A B ) = B T ∂ A ∂ T r ( A B ) = ∂ i = 1 ∑ m j = 1 ∑ n a i j ∂ i = 1 ∑ m j = 1 ∑ n a i j b j i = i = 1 ∑ m j = 1 ∑ n b j i = B T ∂ A ∂ T r ( A B A T C ) = ∂ A ∂ T r ( A T C A B ) = ∂ A ∂ T r ( A C T A T B T ) = C A B + ( B A T C ) T = C A B + C T A B T 若 不 使 用 求 和 符 号 有 些 矩 阵 运 算 很 难 描 述 而 通 过 矩 阵 乘 法 和 迹 运 算 符 号 可 以 清 楚 地 表 示 . 例 如 迹 运 算 提 供 了 另 一 种 描 述 矩 阵 F r o b e n i u s 范 数 的 方 式 : ∣ ∣ A ∣ ∣ F = T r ( A A T )
a = np.mat([
[401, -201],
[-800, 401]
])
np.trace(a)
802
1.3.1 特征值
eigenvalues
A 是n阶方阵 如果存在数m和非零n维列向量 x 使得 Ax=mx 成立 则称 m 是A的一个特征值(characteristic value)或本征值(eigenvalue).
https://baike.baidu.com/item/%E7%89%B9%E5%BE%81%E5%80%BC?fromModule=lemma_search-box
( A − λ I ) X = 0 ∣ a 11 − λ a 12 ⋯ a 1 n a 21 a 22 − λ ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n m − λ ∣ 满 足 以 下 特 性 : λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n λ 1 λ 2 ⋯ λ n = ∣ A ∣ (A - \lambda I)X = 0\\
\left| \begin{matrix} a_{11}-\lambda & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} - \lambda & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} - \lambda \end{matrix} \right| \\
\\
满足以下特性:
\\
\lambda_1+\lambda_2+\cdots+\lambda_n=a_{11}+a_{22}+\cdots+a_{nn}\\
\lambda_1\lambda_2\cdots\lambda_n=|A|
( A − λ I ) X = 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ a 1 1 − λ a 2 1 ⋮ a n 1 a 1 2 a 2 2 − λ ⋮ a n 2 ⋯ ⋯ ⋯ a 1 n a 2 n ⋮ a n m − λ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 满 足 以 下 特 性 : λ 1 + λ 2 + ⋯ + λ n = a 1 1 + a 2 2 + ⋯ + a n n λ 1 λ 2 ⋯ λ n = ∣ A ∣
linalg.eig (a )[source]
返回矩阵特征值和特征向量(标准化之后)
Compute the eigenvalues and right eigenvectors of a square array.
a (…, M, M) array
Matrices for which the eigenvalues and right eigenvectors will be computed
A namedtuple with the following attributes:
eigenvalues (…, M) arrayThe eigenvalues, each repeated according to its multiplicity. The eigenvalues are not necessarily ordered. The resulting array will be of complex type, unless the imaginary part is zero in which case it will be cast to a real type. When a is real the resulting eigenvalues will be real (0 imaginary part) or occur in conjugate pairs.
eigenvectors (…, M, M) arrayThe normalized (unit " length" ) eigenvectors, such that the column eigenvectors[:,i] is the eigenvector corresponding to the eigenvalue eigenvalues[i].
a = np.mat([
[401, -201],
[-800, 401]
])
eigvals, eigvecs = np.linalg.eig(a)
eigvals
array([8.01998753e+02, 1.24688473e-03])
eigvecs(单位向量)
matrix([[ 0.44810624, 0.44810624],
[-0.89398031, 0.89398031]])
# 恢复矩阵
eigvecs * np.diag(eigvals) * eigvecs.I
matrix([[ 401., -201.],
[-800., 401.]])
1.4 行列式
determinants
矩阵行列式是指矩阵的全部元素构成的行列式 设A=(aij)是数域P上的一个n阶矩阵 则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式 记为|A|或det(A). 若A B是数域P上的两个n阶矩阵 k是P中的任一个数 则|AB|=|A||B| |kA|=kⁿ|A| |A*|=|A|n-1 其中A*是A的伴随矩阵; 若A是可逆矩阵 则|A-1|=|A|-1.
https://baike.baidu.com/item/%E7%9F%A9%E9%98%B5%E8%A1%8C%E5%88%97%E5%BC%8F/18882017
存 在 方 阵 A , 常 见 表 示 形 式 : ∣ A ∣ , d e t ( A ) d e t ( A ) = d e t [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] = a 11 A 11 + a 12 A 12 + a 13 A 13 = a 11 ( − 1 ) 1 + 1 ∣ a 22 a 23 a 32 a 33 ∣ + a 12 ( − 1 ) 1 + 2 ∣ a 21 a 23 a 31 a 33 ∣ + a 13 ( − 1 ) 1 + 3 ∣ a 21 a 22 a 31 a 32 ∣ = a 11 ( a 22 a 33 − a 32 a 23 ) − a 12 ( a 21 a 33 − a 31 a 23 ) + a 13 ( a 21 a 32 − a 31 a 22 ) 存 在 以 下 特 性 : d e t ( A ) = d e t ( A T ) A 为 三 角 矩 阵 ( 上 , 下 ) , 则 A 的 行 列 式 等 于 A 的 对 角 元 素 的 乘 积 . A 为 n × n 矩 阵 . ( i ) 若 A 有 一 行 或 一 列 包 含 的 元 素 全 为 零 则 d e t ( A ) = 0. ( i i ) 若 A 有 两 行 或 两 列 相 等 则 d e t ( A ) = 0. 存在方阵A,
常见表示形式: |A|, det(A)\\
det(A)=det \left[\begin{array}{ccc} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{array}\right] =a_{11}A_{11}+a_{12}A_{12}+a_{13}A_{13} \\ =a_{11}(-1)^{1+1}\left|\begin{array}{ccc} a_{22}&a_{23}\\ a_{32}&a_{33} \end{array}\right| + a_{12}(-1)^{1+2}\left|\begin{array}{ccc} a_{21}&a_{23}\\ a_{31}&a_{33} \end{array}\right| + a_{13}(-1)^{1+3}\left|\begin{array}{ccc} a_{21}&a_{22}\\ a_{31}&a_{32} \end{array}\right| \\ =a_{11}(a_{22}a_{33}-a_{32}a_{23})-a_{12}(a_{21}a_{33}-a_{31}a_{23})+a_{13}(a_{21}a_{32}-a_{31}a_{22}) \\
\\
存在以下特性:\\
det(A) = det(A^T)\\
A为三角矩阵(上, 下), 则A的行列式等于A的对角元素的乘积.\\
A为n×n矩阵. \\
(i) 若A有一行或一列包含的元素全为零 则det(A)=0. \\
(ii) 若A有两行或两列相等 则det(A)=0. \\
存 在 方 阵 A , 常 见 表 示 形 式 : ∣ A ∣ , d e t ( A ) d e t ( A ) = d e t ⎣ ⎡ a 1 1 a 2 1 a 3 1 a 1 2 a 2 2 a 3 2 a 1 3 a 2 3 a 3 3 ⎦ ⎤ = a 1 1 A 1 1 + a 1 2 A 1 2 + a 1 3 A 1 3 = a 1 1 ( − 1 ) 1 + 1 ∣ ∣ ∣ ∣ a 2 2 a 3 2 a 2 3 a 3 3 ∣ ∣ ∣ ∣ + a 1 2 ( − 1 ) 1 + 2 ∣ ∣ ∣ ∣ a 2 1 a 3 1 a 2 3 a 3 3 ∣ ∣ ∣ ∣ + a 1 3 ( − 1 ) 1 + 3 ∣ ∣ ∣ ∣ a 2 1 a 3 1 a 2 2 a 3 2 ∣ ∣ ∣ ∣ = a 1 1 ( a 2 2 a 3 3 − a 3 2 a 2 3 ) − a 1 2 ( a 2 1 a 3 3 − a 3 1 a 2 3 ) + a 1 3 ( a 2 1 a 3 2 − a 3 1 a 2 2 ) 存 在 以 下 特 性 : d e t ( A ) = d e t ( A T ) A 为 三 角 矩 阵 ( 上 , 下 ) , 则 A 的 行 列 式 等 于 A 的 对 角 元 素 的 乘 积 . A 为 n × n 矩 阵 . ( i ) 若 A 有 一 行 或 一 列 包 含 的 元 素 全 为 零 则 d e t ( A ) = 0 . ( i i ) 若 A 有 两 行 或 两 列 相 等 则 d e t ( A ) = 0 .
# numpy中进行行列式计算
np.linalg.det(np.mat([
[1, 2],
[2, 4]
]))
0
# 转置后, 依然为0
np.linalg.det(np.mat([
[1, 2],
[2, 4]
]).T)
1.4.1 向量
vector
向量空间( 也称为线性空间) 是称为对象的集合的载体 其可被添加在一起 并乘以由数字( " 缩放" ) 所谓的标量. 标量通常被认为是实数 但是也存在标量乘以复数 有理数或通常任何字段的向量空间. 向量加法和标量乘法的运算必须满足下面列出的某些要求 称为公理.
欧几里德向量是向量空间的一个例子. 它们代表物理量 诸如力: 任何两个力( 同一类型的) 可被添加 以产生第三和的相乘力矢量由一实数乘法器是另一个力矢量. 同样 但在更几何意义上 表示平面或三维空间中的位移的矢量也形成矢量空间. 向量空间中的向量不一定必须是箭头状对象 因为它们出现在上述示例中: 向量被视为具有特定属性的抽象数学对象 在某些情况下可以将其视为箭头.
向量空间是线性代数的主题 并且通过它们的维度很好地表征 粗略地说 它指定了空间中独立方向的数量. 无限维向量空间在数学分析中自然出现 作为函数空间 其向量是函数. 这些向量空间通常具有附加结构 其可以是拓扑结构 允许考虑接近度和连续性问题. 在这些拓扑中 由规范或内积定义的拓扑更常用 因为它具有距离概念两个向量之间. 特别是Banach空间和Hilbert 空间的情况 这是数学分析的基础.
https://en.wikipedia.org/wiki/Vector_space
(图: 见水印 )
以下内容引用自: 清雅白鹿记 - 知乎 (zhihu.com)
A d ⃗ = [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] [ d 1 d 2 d 3 ] = d 1 [ a 1 a 2 a 3 ] + d 2 [ b 1 b 2 b 3 ] + d 3 [ c 1 c 2 c 3 ] = d 1 a ⃗ + d 2 b ⃗ + d 3 c ⃗ = [ n 1 n 2 n 3 ] = n ⃗ \begin{aligned}
A\vec d &=
\begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{bmatrix}
\begin{bmatrix} d_1 \\ d_2 \\d_3 \end{bmatrix} \\ &= d_1
\begin{bmatrix} a_1 \\ a_2 \\a_3 \end{bmatrix} +d_2
\begin{bmatrix} b_1 \\ b_2 \\b_3 \end{bmatrix} + d_3
\begin{bmatrix} c_1 \\ c_2 \\c_3 \end{bmatrix} \\ &= d_1 \vec a + d_2 \vec b + d_3 \vec c \\ &= \begin{bmatrix} n_1 \\ n_2 \\n_3 \end{bmatrix}= \vec n \end{aligned}\\
\\
A d = ⎣ ⎡ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ⎦ ⎤ ⎣ ⎡ d 1 d 2 d 3 ⎦ ⎤ = d 1 ⎣ ⎡ a 1 a 2 a 3 ⎦ ⎤ + d 2 ⎣ ⎡ b 1 b 2 b 3 ⎦ ⎤ + d 3 ⎣ ⎡ c 1 c 2 c 3 ⎦ ⎤ = d 1 a + d 2 b + d 3 c = ⎣ ⎡ n 1 n 2 n 3 ⎦ ⎤ = n
d ⃗ 在 由 矩 阵 A 映 射 前 后 两 个 坐 标 系 下 的 坐 标 [ d 1 d 2 d 3 ] , [ n 1 n 2 n 3 ] 之 间 的 关 系 是 : [ n 1 n 2 n 3 ] = A [ d 1 d 2 d 3 ] d ⃗ 被 映 射 到 A 的 列 向 量 , a ⃗ , b ⃗ , c ⃗ 所 张 成 的 三 维 空 间 中 的 n ⃗ \vec d在由矩阵A映射前后两个坐标系下的坐标\begin{bmatrix}d_1 \\ d_2 \\d_3 \end{bmatrix},\quad \begin{bmatrix} n_1 \\ n_2 \\n_3 \end{bmatrix}之间的关系是:\\
\begin{bmatrix} n_1 \\ n_2 \\n_3 \end{bmatrix} = A \begin{bmatrix} d_1 \\ d_2 \\d_3 \end{bmatrix}\\
\vec d 被映射到A的列向量, \vec a,\quad \vec b,\quad\vec c所张成的三维空间中的\vec n
d 在 由 矩 阵 A 映 射 前 后 两 个 坐 标 系 下 的 坐 标 ⎣ ⎡ d 1 d 2 d 3 ⎦ ⎤ , ⎣ ⎡ n 1 n 2 n 3 ⎦ ⎤ 之 间 的 关 系 是 : ⎣ ⎡ n 1 n 2 n 3 ⎦ ⎤ = A ⎣ ⎡ d 1 d 2 d 3 ⎦ ⎤ d 被 映 射 到 A 的 列 向 量 , a , b , c 所 张 成 的 三 维 空 间 中 的 n
1阶行列式|a|表示一维坐标轴上的有向长度.
2阶行列式表示2个行向量为邻边构成的平行四边形的有向面积;
3阶行列式表示其行向量或列向量所张成的平行六面体的有向体积
n阶行列式det A , 表示矩阵A对应的线性变换前后的面积或体积比, 还可以表示其行向量或列向量所张成的超平行多面体的有向体积.
1.5 Python原生矩阵的实现
class Matrix:
def __init__(self, matrix):
self.values = matrix
def __matmul__(self, other):
# 乘法, 其他运算类似操作
a = self.values
b = other.values
return [
[
sum([float(i) * float(j) for i, j in zip(row, col)])
for col in zip(*b)
]
for row in a
]
A = [[1,2,3],[4,5,6]]
B = [[1,1], [1,1], [1,1]]
# @, 矩阵乘法的专属操作符
Matrix(A) @ Matrix(B)
[[6.0, 6.0], [15.0, 15.0]]
import numpy as np
a = np.mat(A)
b = np.mat(B)
a * b
matrix([[ 6, 6],
[15, 15]])
二. 基本运算
2.1 加
A m × n + B m × n = M m × n 常 见 特 性 : A + B = B + A ( A + B ) + C = A + ( B + C ) A_{m \times n} + B_{m \times n} = M_{m \times n}\\
\\
常见特性:\\
\mathbf{A} + \mathbf{B} = \mathbf{B} + \mathbf{A}\\
\left ( \mathbf{A} + \mathbf{B}\right ) + \mathbf{C} = \mathbf{A} + \left ( \mathbf{B} + \mathbf{C} \right )
A m × n + B m × n = M m × n 常 见 特 性 : A + B = B + A ( A + B ) + C = A + ( B + C )
2.2 乘
A m × p ∗ B p × n = M m × n A_{m \times p} * B_{p \times n} = M_{m \times n}
A m × p ∗ B p × n = M m × n
a.shape
(2, 3)
b.shape
(3, 2)
乘 法 常 见 特 性 : ( A B ) C = A ( B C ) ( A + B ) C = A C + B C C ( A + B ) = C A + C B k ( A B ) = ( k A ) B = A ( k B ) 乘法常见特性:\\
(AB)C = A(BC)\\
(A + B)C = AC + BC\\
C(A+B)=CA+CB\\
k(AB) =(kA)B=A(kB)\\
乘 法 常 见 特 性 : ( A B ) C = A ( B C ) ( A + B ) C = A C + B C C ( A + B ) = C A + C B k ( A B ) = ( k A ) B = A ( k B )
三. 转置
transpose
A m × n = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n … a m 1 a m 2 … a m n ] A T n × m = [ a 11 a 21 … a m 1 a 12 a 22 … a m 2 … a 1 n a 2 n … a m n ] ( A B ) T = B T A T ( A + B ) T = A T + B T ( k A ) T = k A T ( A T ) T = A ( A 1 A 2 . . A n ) T = A n T . . A 2 T A 1 T \underset{m\times n}{\mathbf{A}} = \begin{bmatrix}a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mn}\end{bmatrix}\\
\\
\underset{n\times m}{A^{T}} = \begin{bmatrix}a_{11} & a_{21} & \ldots & a_{m1} \\ a_{12} & a_{22} & \ldots & a_{m2} \\ \ldots \\ a_{1n} & a_{2n} & \ldots & a_{mn}\end{bmatrix}\\
\\
(AB)^T=B^TA^T\\
(A + B) ^ T = A^T + B^T\\
(k\mathbf{A})^{T}=k\mathbf{A}^{T}\\
(\mathbf{A}^{T})^{T}=\mathbf{A}\\
(A_1A_2..A_n)^T = A_n^T..A_2^TA_1^T\\
m × n A = ⎣ ⎢ ⎢ ⎡ a 1 1 a 2 1 … a m 1 a 1 2 a 2 2 a m 2 … … … a 1 n a 2 n a m n ⎦ ⎥ ⎥ ⎤ n × m A T = ⎣ ⎢ ⎢ ⎡ a 1 1 a 1 2 … a 1 n a 2 1 a 2 2 a 2 n … … … a m 1 a m 2 a m n ⎦ ⎥ ⎥ ⎤ ( A B ) T = B T A T ( A + B ) T = A T + B T ( k A ) T = k A T ( A T ) T = A ( A 1 A 2 . . A n ) T = A n T . . A 2 T A 1 T
3.1 转置共轭
Conjugate transpose
共轭转置 一般指的是m*n型矩阵A做的一种数学变换 其中矩阵A中的任一元素a_ij属于复数域C. 符号: 与普通转置右角标T相对应 通常用H右角标或*右角标来表示共轭转置 共轭转置后的矩阵A^H称为A的共轭转置矩阵 A^H为n*m型. 具体操作方法: 首先将A中的每个元素a_ij取共轭得b_ij 将新得到的由b_ij组成的新m*n型矩阵记为矩阵B再对矩阵B作普通转置得到B^T即为A的共轭转置矩阵: B ^ T=A ^ H
共轭转置_百度百科 (baidu.com)
一般来讲A^T表示转置 A^H表示转置共轭, 对实矩阵而言是一回事, 对复矩阵而言转置共轭比单纯的转置更常用一些 比如酉变换, Hermite型等.
四. 逆矩阵
inverse.
可逆条件
矩阵A可逆的充要条件是A的行列式不等于0.
可逆矩阵一定是方阵.
如果矩阵A是可逆的 A的逆矩阵是唯一的.
可逆矩阵也被称为非奇异矩阵 满秩矩阵.
两个可逆矩阵的乘积依然可逆.
可逆矩阵的转置矩阵也可逆.
矩阵可逆当且仅当它是满秩矩阵.
作者: horu
逆 矩 阵 : A B = B A = I A = B − 1 B = A − 1 ( A B ) − 1 = B − 1 A − 1 , A , B 同 阶 , 可 逆 ( A − 1 ) T = ( A T ) − 1 双 侧 可 逆 : A A − 1 = I = A − 1 A ; 左 侧 可 逆 : A l e f t − 1 A = I ≠ A A l e f t − 1 ; 右 侧 可 逆 : A A r i g h t − 1 = I ≠ A r i g h t − 1 A ; 逆矩阵: AB = BA = I\\
A = B ^{-1}\\
B = A ^{-1}\\
(AB) ^{-1} = B^{-1}A^{-1}, A, B同阶, 可逆\\
(A^{-1})^T=(A^T)^{-1}\\
双侧可逆:AA^{-1} = I = A^{-1}A;\\
左侧可逆:A^{-1}_{left}A = I \neq AA^{-1}_{left};\\
右侧可逆: AA^{-1}_{right} = I \neq A^{-1}_{right}A;
逆 矩 阵 : A B = B A = I A = B − 1 B = A − 1 ( A B ) − 1 = B − 1 A − 1 , A , B 同 阶 , 可 逆 ( A − 1 ) T = ( A T ) − 1 双 侧 可 逆 : A A − 1 = I = A − 1 A ; 左 侧 可 逆 : A l e f t − 1 A = I = A A l e f t − 1 ; 右 侧 可 逆 : A A r i g h t − 1 = I = A r i g h t − 1 A ;
4.1 伪逆矩阵
Pseudoinverse Matrix, 或者称为广义逆矩阵.
奇异矩阵和非方阵没有逆矩阵 但可以有伪逆矩阵.
满 足 以 下 特 性 : x = p i n v ( A ) ; x ∗ A ∗ x = x A ∗ x ∗ A = A 满足以下特性:\\
x = pinv(A);\\
x * A * x = x\\
A * x * A = A
满 足 以 下 特 性 : x = p i n v ( A ) ; x ∗ A ∗ x = x A ∗ x ∗ A = A
4.2 inv & pinv
Compute the (multiplicative) inverse of a matrix.
Given a square matrix a , return the matrix ainv satisfying dot(a, ainv) = dot(ainv, a) = eye(a.shape[0]).
https://numpy.org/doc/stable/reference/generated/numpy.linalg.inv.html
Compute the (Moore-Penrose) pseudo-inverse of a matrix.
Calculate the generalized inverse of a matrix using its singular-value decomposition (SVD) and including all large singular values.
https://numpy.org/doc/stable/reference/generated/numpy.linalg.pinv.html
import numpy as np
m = np.mat([
[1, 2],
[3, 4]
])
m.I
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
np.linalg.inv(m)
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
np.linalg.pinv(m)
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
m * m.I
matrix([[1.00000000e+00, 1.11022302e-16],
[0.00000000e+00, 1.00000000e+00]])
# 构造一个不可逆的矩阵
n = np.mat([
[1, 2],
[2, 4]
])
n.I
---------------------------------------------------------------------------
LinAlgError
np.linalg.pinv(n)
matrix([[0.04, 0.08],
[0.08, 0.16]])
n * np.linalg.pinv(n)
matrix([[0.2, 0.4],
[0.4, 0.8]])
n * np.linalg.pinv(n)*n
matrix([[1., 2.],
[2., 4.]])
np.linalg.pinv(n) * n * np.linalg.pinv(n)
matrix([[0.04, 0.08],
[0.08, 0.16]])
4.3 奇异矩阵
奇异矩阵是线性代数的概念, 就是该 矩阵的秩不是满秩. 首先, 看这个矩阵是不是方阵(即行数和列数相等的矩阵, 若行数和列数不相等, 那就谈不上奇异矩阵和 非奇异矩阵 ). 然后, 再看此矩阵的 行列式 |A|是否等于0, 若等于0, 称矩阵A为奇异矩阵; 若不等于0, 称矩阵A为非奇异矩阵. 同时, 由|A|≠0可知矩阵A可逆, 这样可以得出另外一个重要结论: 可逆矩阵 就是非奇异矩阵, 非奇异矩阵也是可逆矩阵. 如果A为奇异矩阵, 则AX=0有无穷解, AX=b有无穷解或者无解. 如果A为非奇异矩阵, 则AX=0有且只有唯一 零解 , AX=b有唯一解.
# 计算上述的n矩阵
np.linalg.det(n)
0
4.4 OLS
在之前的文章, 最小二乘的的normal equations:
w ^ ∗ = ( X T X ) − 1 X T y = X − 1 ( X T ) − 1 X T y \hat{w}^* = (X^TX)^{-1}X^Ty\\
= X^{-1}(X^T)^{-1}X^Ty
w ^ ∗ = ( X T X ) − 1 X T y = X − 1 ( X T ) − 1 X T y
import numpy as np
y =np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
])
y = y[:, np.newaxis]
x = np.array([[e, 1] for e in range(1, 21)])
np.linalg.lstsq(x, y, rcond=1e-5)
(array([[0.96992481],
[0.51578947]]),
array([40.59849624]),
2,
array([53.71583167, 2.14695784]))
# 使用逆矩阵求解
np.linalg.pinv(x).dot(y)
array([[0.96992481],
[0.51578947]])
np.mat(x).I*np.mat(y)
matrix([[0.96992481],
[0.51578947]])
矩 阵 A 伪 逆 : A + = lim α → 0 ( A T A + α I ) − 1 A T = V D + U T 其 中 矩 阵 U D V 是 矩 阵 奇 异 值 分 解 后 得 到 的 矩 阵 . 对 角 矩 阵 D 的 伪 逆 D + 是 其 非 零 元 素 取 倒 数 之 后 再 转 置 得 到 的 . 当 矩 阵 A 的 列 数 多 于 行 数 时 使 用 伪 逆 求 解 线 性 方 程 是 众 多 可 能 解 法 中 的 一 种 . 特 别 的 , x = A + y 是 方 程 所 有 可 行 解 中 欧 几 里 得 范 数 ∣ ∣ x ∣ ∣ 2 最 小 的 一 个 . 当 矩 阵 A 的 行 数 多 于 列 数 时 可 能 没 解 . 在 这 种 情 况 下 通 过 伪 逆 得 到 的 x 使 得 A x 和 y 的 欧 几 里 得 距 离 ∣ ∣ A x − y ∣ ∣ 2 最 小 . 矩阵A伪逆: A^+ = \lim_{\alpha\rightarrow 0}(A^TA + \alpha I)^{-1}A^T\\
= VD^+U^T\\
其中 矩阵U D V是矩阵奇异值分解后得到的矩阵.\\
对角矩阵D的伪逆D^+是其非零元素取倒数之后再转置得到的.\\
当矩阵A的列数多于行数时 使用伪逆求解线性方程是众多可能解法中的一种. \\
特别的, x = A^+y是方程所有可行解中欧几里得范数||x||_2最小的一个.\\
当矩阵A的行数多于列数时 可能没解. \\
在这种情况下 通过伪逆得到的x使得Ax和y的欧几里得距离||Ax - y||_2最小.
矩 阵 A 伪 逆 : A + = α → 0 lim ( A T A + α I ) − 1 A T = V D + U T 其 中 矩 阵 U D V 是 矩 阵 奇 异 值 分 解 后 得 到 的 矩 阵 . 对 角 矩 阵 D 的 伪 逆 D + 是 其 非 零 元 素 取 倒 数 之 后 再 转 置 得 到 的 . 当 矩 阵 A 的 列 数 多 于 行 数 时 使 用 伪 逆 求 解 线 性 方 程 是 众 多 可 能 解 法 中 的 一 种 . 特 别 的 , x = A + y 是 方 程 所 有 可 行 解 中 欧 几 里 得 范 数 ∣ ∣ x ∣ ∣ 2 最 小 的 一 个 . 当 矩 阵 A 的 行 数 多 于 列 数 时 可 能 没 解 . 在 这 种 情 况 下 通 过 伪 逆 得 到 的 x 使 得 A x 和 y 的 欧 几 里 得 距 离 ∣ ∣ A x − y ∣ ∣ 2 最 小 .
详细的矩阵推导过程见下面的矩阵推导部分的内容.
五. 特殊矩阵
5.1 单位矩阵
identity matrix
单位矩阵:(一般使用I, E来表示) I = [ 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 ] 任 意 的 矩 阵 相 乘 I A = A I = A 单 位 矩 阵 的 逆 矩 阵 是 其 本 身 . \text{单位矩阵:(一般使用I, E来表示)}\\
I= \begin{bmatrix}
1 & 0 & \cdots & 0\\
0 & 1 & \cdots & 0\\
\vdots&\vdots & \ddots & \vdots\\
0 & 0 & \cdots & 1
\end{bmatrix}\\\\
任意的矩阵相乘 IA = AI = A\\
单位矩阵的逆矩阵是其本身.
单位矩阵 :( 一般使用 I, E 来表示 ) I = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 ⋮ 0 0 1 ⋮ 0 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ 1 ⎦ ⎥ ⎥ ⎥ ⎤ 任 意 的 矩 阵 相 乘 I A = A I = A 单 位 矩 阵 的 逆 矩 阵 是 其 本 身 .
5.2 对角矩阵
diagonal matrix
也成为: 缩放矩阵
除 了 对 角 线 之 外 的 元 素 全 部 为 0. A = [ a 11 a 22 a 33 a 44 ] , 常 见 表 示 d i a g ( a 11 , a 22 . . . ) = A 对 角 矩 阵 的 转 置 等 于 自 身 : A T = A [ a 0 0 0 0 b 0 0 0 0 c 0 0 0 0 d ] [ 1 a 0 0 0 0 1 b 0 0 0 0 1 c 0 0 0 0 1 d ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] 若 对 角 矩 阵 的 对 角 线 上 含 有 值 为 0 的 元 素 , 则 该 对 角 矩 阵 不 可 逆 [ a 0 0 0 a 0 0 0 a ] [ h i j l m n o p q ] = [ h i j l m n o p q ] [ a 0 0 0 a 0 0 0 a ] = a ∗ [ h i j l m n o p q ] = [ a h a i a j a l a m a n a o a p a q ] 常 数 : ( a A ) T = A T a = a A T 两 个 对 角 矩 阵 A m × p ∗ B p × n = M m × n , M m × n 也 为 对 角 矩 阵 缩 放 的 来 源 : 实 现 对 x , y 的 m , n 倍 的 缩 放 [ m 0 0 n ] [ x y ] = [ m ∗ x n ∗ y ] 除了对角线之外的元素全部为0.\\
A = \begin{bmatrix}
a_{11} & & & \\
& a_{22} & & \\
& & a_{33}&\\
& & &a_{44}
\end{bmatrix}, \;常见表示diag(a_{11}, a_{22}...) = A\\
对角矩阵的转置等于自身: A^T = A\\
\begin{bmatrix} a & 0&0&0\\ 0 & b&0&0\\ 0 &0&c&0\\ 0 & 0&0&d \end{bmatrix} \begin{bmatrix} \frac{1}{a} & 0&0&0\\ 0 & \frac{1}{b}&0&0\\ 0 &0&\frac{1}{c}&0\\ 0 & 0&0&\frac{1}{d} \end{bmatrix} =\begin{bmatrix} 1& 0&0&0\\ 0 & 1&0&0\\ 0 &0&1&0\\ 0 & 0&0&1 \end{bmatrix}\\
若对角矩阵的对角线上含有值为0的元素, 则该对角矩阵不可逆\\\\
\begin{bmatrix} a & 0&0\\ 0 & a&0\\ 0 &0&a \end{bmatrix} \begin{bmatrix} h & i&j\\ l& m&n\\ o &p&q\end{bmatrix}=\begin{bmatrix} h & i&j\\ l& m&n\\ o &p&q\end{bmatrix}\begin{bmatrix} a & 0&0\\ 0 & a&0\\ 0 &0&a \end{bmatrix} =a*\begin{bmatrix} h & i&j\\ l& m&n\\ o &p&q\end{bmatrix} =\begin{bmatrix} ah & ai&aj\\ al& am&an\\ ao &ap&aq\end{bmatrix}\\
常数: (a\bold{A})^T=\bold{A}^Ta=a\bold{A}^T\\
\\
两个对角矩阵A_{m \times p} * B_{p \times n} = M_{m \times n}, M_{m \times n}也为对角矩阵\\
缩放的来源:实现对x, y的m, n倍的缩放\\
\begin{bmatrix} m & 0\\ 0 & n \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} =\begin{bmatrix} m* x\\ n * y \end{bmatrix}\\
除 了 对 角 线 之 外 的 元 素 全 部 为 0 . A = ⎣ ⎢ ⎢ ⎡ a 1 1 a 2 2 a 3 3 a 4 4 ⎦ ⎥ ⎥ ⎤ , 常 见 表 示 d i a g ( a 1 1 , a 2 2 . . . ) = A 对 角 矩 阵 的 转 置 等 于 自 身 : A T = A ⎣ ⎢ ⎢ ⎡ a 0 0 0 0 b 0 0 0 0 c 0 0 0 0 d ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ a 1 0 0 0 0 b 1 0 0 0 0 c 1 0 0 0 0 d 1 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ 若 对 角 矩 阵 的 对 角 线 上 含 有 值 为 0 的 元 素 , 则 该 对 角 矩 阵 不 可 逆 ⎣ ⎡ a 0 0 0 a 0 0 0 a ⎦ ⎤ ⎣ ⎡ h l o i m p j n q ⎦ ⎤ = ⎣ ⎡ h l o i m p j n q ⎦ ⎤ ⎣ ⎡ a 0 0 0 a 0 0 0 a ⎦ ⎤ = a ∗ ⎣ ⎡ h l o i m p j n q ⎦ ⎤ = ⎣ ⎡ a h a l a o a i a m a p a j a n a q ⎦ ⎤ 常 数 : ( a A ) T = A T a = a A T 两 个 对 角 矩 阵 A m × p ∗ B p × n = M m × n , M m × n 也 为 对 角 矩 阵 缩 放 的 来 源 : 实 现 对 x , y 的 m , n 倍 的 缩 放 [ m 0 0 n ] [ x y ] = [ m ∗ x n ∗ y ]
5.3 正交矩阵
orthogonal matrix
A T A = I , 则 称 A 为 正 交 矩 阵 . 正 交 矩 阵 A 的 逆 矩 阵 A − 1 = A T , 即 A A − 1 = I A = [ a b c d ] A T = [ a c b d ] A A T = [ a a + b b a c + b d c a + d b c c + d d ] = [ 1 0 0 1 ] 即 : a c + b d = c a + b d = 0 , a a + b b = c c + d d = 1 A 按 行 取 向 量 : i ⃗ = ( a , b ) j ⃗ = ( c , d ) i ⃗ ⋅ j ⃗ = a c + b d = 0 ∣ i ⃗ ∣ = a a + b b = 1 , i ⃗ 的 模 长 为 1 , 单 位 向 量 ; 同 理 j ⃗ = 1 A^TA = I, 则称A为正交矩阵.\\
正交矩阵A的逆矩阵A^{-1} = A^T, 即\;AA^{-1} = I
\\
\mathbf{A} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\\
\mathbf{A}^{T} = \begin{bmatrix} a & c \\ b & d \end{bmatrix}\\
\mathbf{A} \mathbf{A}^{T} = \begin{bmatrix} aa+bb & ac+bd \\ ca+db & cc+dd \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\\
即: ac+bd=ca+bd = 0, aa+bb=cc+dd= 1\\
\\
A按行取向量:\\
\vec{i}=(a,b)\\
\vec{j}=(c,d)\\
\vec{i}\cdot \vec{j}=ac+bd = 0\\
| \vec{i} |=\sqrt{aa+bb} = 1, \vec{i}的模长为\: 1, 单位向量; 同理\vec{j} = 1\\
A T A = I , 则 称 A 为 正 交 矩 阵 . 正 交 矩 阵 A 的 逆 矩 阵 A − 1 = A T , 即 A A − 1 = I A = [ a c b d ] A T = [ a b c d ] A A T = [ a a + b b c a + d b a c + b d c c + d d ] = [ 1 0 0 1 ] 即 : a c + b d = c a + b d = 0 , a a + b b = c c + d d = 1 A 按 行 取 向 量 : i = ( a , b ) j = ( c , d ) i ⋅ j = a c + b d = 0 ∣ i ∣ = a a + b b = 1 , i 的 模 长 为 1 , 单 位 向 量 ; 同 理 j = 1
5.4 三角矩阵
A = [ a 11 a 12 ⋯ a 1 n a 22 ⋯ a 2 n ⋱ ⋮ a n n ] 分 为 上 三 角 , 对 角 线 下 方 的 元 素 全 部 为 0 ; 下 三 角 , 对 角 线 上 方 的 元 素 为 0. 上 三 角 的 转 置 为 下 三 角 , 反 之 亦 然 . 三 角 矩 阵 的 行 列 式 等 于 角 线 上 元 素 的 积 . A=
\left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
&a_{22} & \cdots &a_{2n} \\
& & \ddots & \vdots \\
&
& &a_{nn}
\end{array}\right]\\
分为上三角, 对角线下方的元素全部为0; 下三角, 对角线上方的元素为0.\\
上三角的转置为下三角, 反之亦然.\\
三角矩阵的行列式等于角线上元素的积.\\
A = ⎣ ⎢ ⎢ ⎢ ⎡ a 1 1 a 1 2 a 2 2 ⋯ ⋯ ⋱ a 1 n a 2 n ⋮ a n n ⎦ ⎥ ⎥ ⎥ ⎤ 分 为 上 三 角 , 对 角 线 下 方 的 元 素 全 部 为 0 ; 下 三 角 , 对 角 线 上 方 的 元 素 为 0 . 上 三 角 的 转 置 为 下 三 角 , 反 之 亦 然 . 三 角 矩 阵 的 行 列 式 等 于 角 线 上 元 素 的 积 .
5.5 对称矩阵
5.5.1 对角矩阵
A = [ λ 11 λ 22 λ 33 λ 44 ] , 常 见 表 示 d i a g ( λ 11 , λ 22 . . . ) = A 对 角 矩 阵 , 除 了 主 对 角 的 元 素 , 其 他 为 0 , 主 对 角 线 中 其 他 元 素 可 以 为 0. 当 对 角 线 元 素 为 1 , 即 为 单 位 矩 阵 . A = \begin{bmatrix}
\lambda_{11} & & & \\
& \lambda_{22} & & \\
& & \lambda_{33}&\\
& & &\lambda_{44}
\end{bmatrix}, \;常见表示diag(\lambda_{11}, \lambda_{22}...) = A\\
对角矩阵, 除了主对角的元素, 其他为0, 主对角线中其他元素可以为0.
当对角线元素为1, 即为单位矩阵.
A = ⎣ ⎢ ⎢ ⎡ λ 1 1 λ 2 2 λ 3 3 λ 4 4 ⎦ ⎥ ⎥ ⎤ , 常 见 表 示 d i a g ( λ 1 1 , λ 2 2 . . . ) = A 对 角 矩 阵 , 除 了 主 对 角 的 元 素 , 其 他 为 0 , 主 对 角 线 中 其 他 元 素 可 以 为 0 . 当 对 角 线 元 素 为 1 , 即 为 单 位 矩 阵 .
A T = A , A 为 对 称 矩 阵 , 一 定 存 在 正 交 矩 阵 P , 对 角 矩 阵 Λ , 满 足 以 下 : P − 1 A P = Λ A^T = A, A为对称矩阵, 一定存在正交矩阵P, 对角矩阵\Lambda, 满足以下:\\
P^{-1}AP=\Lambda
A T = A , A 为 对 称 矩 阵 , 一 定 存 在 正 交 矩 阵 P , 对 角 矩 阵 Λ , 满 足 以 下 : P − 1 A P = Λ
5.6 Hermite矩阵
A H = A 特 征 值 都 是 实 数 任 意 两 个 不 同 特 征 值 所 对 应 的 特 征 向 量 正 交 A^H=A\\
特征值都是实数\\
任意两个不同特征值所对应的特征向量正交\\
A H = A 特 征 值 都 是 实 数 任 意 两 个 不 同 特 征 值 所 对 应 的 特 征 向 量 正 交
n阶复方阵U的n个列向量 是U空间的一个标准正交基 则U是酉矩阵(Unitary Matrix). 显然酉矩阵是正交矩阵 往复数域上的推广.
A H A = A H A = I A^HA = A^HA = I
A H A = A H A = I
5.8 正定矩阵
positive definite matrix
在线性代数里 正定矩阵 (positive definite matrix) 有时会简称为正定阵. 在线性代数中 正定矩阵的性质类似复数 中的正 实数 . 与正定矩阵相对应的线性算子 是对称 正定双线性形式( 复域中则对应埃尔米特 正定双线性形式 ) .
( 1) 正定矩阵的行列式恒为正;
( 2) 实对称矩阵A正定当且仅当A与单位矩阵合同;
( 3) 若A是正定矩阵 则A的逆矩阵也是正定矩阵;
( 4) 两个正定矩阵的和是正定矩阵;
( 5) 正实数与正定矩阵的乘积是正定矩阵.
https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459
六. 范数
norm
范数 是具有" 长度" 概念的函数. 在线性代数 泛函分析及相关的数学领域 范数是一个函数 是矢量空间内的所有矢量赋予非零的正长度或大小. 半范数可以为非零的矢量赋予零长度. 定义范数的矢量空间是赋范矢量空间; 同样 定义半范数的矢量空间就是赋半范矢量空间. 注: 在二维的欧氏几何空间 R中定义欧氏范数 在该矢量空间中 元素被画成一个从原点出发的带有箭头的有向线段 每一个矢量的有向线段的长度即为该矢量的欧氏范数.
https://baike.baidu.com/item/%E8%8C%83%E6%95%B0
L 0 范 数 ( 0 范 数 ) : ∣ ∣ x ∣ ∣ 0 = 非 零 元 素 的 个 数 ; L 1 范 数 ( 和 范 数 或 1 范 数 ) : ∣ ∣ x ∣ ∣ 1 = ∑ i = 1 m ∣ x i ∣ = ∣ x 1 ∣ + ⋅ ⋅ ⋅ + ∣ x m ∣ L 2 范 数 ( E u c l i d e a n 范 数 , F r o b e n i u s 范 数 ) : ∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ⋅ ⋅ ⋅ + ∣ x m ∣ 2 ) 1 2 L 2 范 数 , 最 为 常 见 L ∞ 范 数 ( 极 大 范 数 , 无 穷 大 范 数 ) : ∣ ∣ x ∣ ∣ ∞ = m a x { ∣ x 1 ∣ , ⋅ ⋅ ⋅ , ∣ x m ∣ } L_0范数(0范数): ||x||_0 = 非零元素的个数;\\
L_1范数(和范数或1范数): \left| \left| x \right| \right|_{1}=\sum_{i=1}^{m}{\left| x_{i} \right|}=\left| x_{1} \right|+\cdot\cdot\cdot+\left| x_{m} \right|\\
L_2范数(Euclidean范数, Frobenius范数): \left| \left| x \right| \right|_{2} = (\left| x_{1} \right|^{2}+\cdot\cdot\cdot+\left| x_{m} \right|^{2})^{\frac{1}{2}}\\
L_2范数, 最为常见\\
L_{\infty}范数(极大范数, 无穷大范数): \left| \left| x \right| \right|_{\infty}=max\left\{ \left| x_{1} \right| ,\cdot\cdot\cdot, \left| x_{m} \right| \right\}\\
L 0 范 数 ( 0 范 数 ) : ∣ ∣ x ∣ ∣ 0 = 非 零 元 素 的 个 数 ; L 1 范 数 ( 和 范 数 或 1 范 数 ) : ∣ ∣ x ∣ ∣ 1 = i = 1 ∑ m ∣ x i ∣ = ∣ x 1 ∣ + ⋅ ⋅ ⋅ + ∣ x m ∣ L 2 范 数 ( E u c l i d e a n 范 数 , F r o b e n i u s 范 数 ) : ∣ ∣ x ∣ ∣ 2 = ( ∣ x 1 ∣ 2 + ⋅ ⋅ ⋅ + ∣ x m ∣ 2 ) 2 1 L 2 范 数 , 最 为 常 见 L ∞ 范 数 ( 极 大 范 数 , 无 穷 大 范 数 ) : ∣ ∣ x ∣ ∣ ∞ = m a x { ∣ x 1 ∣ , ⋅ ⋅ ⋅ , ∣ x m ∣ }
七. 病态矩阵
假 设 有 这 样 的 线 性 方 程 : [ 400 − 200 − 800 401 ] [ x 1 x 2 ] = [ 200 − 200 ] 假设有这样的线性方程:\\
\begin{bmatrix}
400& -200\\
-800 & 401
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix} =
\begin{bmatrix}
200\\
-200
\end{bmatrix}
假 设 有 这 样 的 线 性 方 程 : [ 4 0 0 − 8 0 0 − 2 0 0 4 0 1 ] [ x 1 x 2 ] = [ 2 0 0 − 2 0 0 ]
import numpy as np
a = np.mat([
[400, -201],
[-800, 401]
])
b = np.mat([
[200],
[-200]
])
np.linalg.solve(a, b)
matrix([[-100.],
[-200.]])
对 上 面 的 方 程 进 行 轻 微 的 改 动 : [ 401 − 200 − 800 401 ] [ x 1 x 2 ] = [ 200 − 200 ] 对上面的方程进行轻微的改动:\\
\begin{bmatrix}
401& -200\\
-800 & 401
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix} =
\begin{bmatrix}
200\\
-200
\end{bmatrix}
对 上 面 的 方 程 进 行 轻 微 的 改 动 : [ 4 0 1 − 8 0 0 − 2 0 0 4 0 1 ] [ x 1 x 2 ] = [ 2 0 0 − 2 0 0 ]
# 将400改成401
a = np.mat([
[401, -201],
[-800, 401]
])
np.linalg.solve(a, b)
# 得到新的解和原来的解, 将发生巨大的改变, 虽然只是简单改动一个数
matrix([[40000.00000034],
[79800.00000068]])
假如出现上述的情形, 则称这样的方程组/矩阵为病态的 (ill-conditioned).
八. 矩阵求导
E w ^ = ( y − X w ^ ) T ( y − X w ^ ) 展 开 上 述 式 子 : E w ^ = y T y − y T X w ^ − w ^ T X T y + w ^ T X T X w ^ 求 导 : ∂ E w ^ ∂ w ^ = ∂ y T y ∂ w ^ − ∂ y T X w ^ ∂ w ^ − ∂ w ^ T X T y ∂ w ^ + ∂ w ^ T X T X w ^ ∂ w ^ E_{\hat{w}} = (y - X\hat{w})^T(y - X\hat{w})\\
\\
展开上述式子:\\
E_{\hat{w}} = y^Ty - y^TX\hat{w} -\hat{w}^TX^Ty + \hat{w}^TX^TX\hat{w}\\
求导:\\
\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = \frac{\partial y^Ty }{\partial \hat{w}} - \frac{\partial y^TX\hat{w} }{\partial \hat{w}} - \frac{\partial \hat{w}^TX^Ty }{\partial \hat{w}} + \frac{\partial \hat{w}^TX^TX\hat{w} }{\partial \hat{w}}\\
E w ^ = ( y − X w ^ ) T ( y − X w ^ ) 展 开 上 述 式 子 : E w ^ = y T y − y T X w ^ − w ^ T X T y + w ^ T X T X w ^ 求 导 : ∂ w ^ ∂ E w ^ = ∂ w ^ ∂ y T y − ∂ w ^ ∂ y T X w ^ − ∂ w ^ ∂ w ^ T X T y + ∂ w ^ ∂ w ^ T X T X w ^
∂ E w ^ ∂ w ^ = ∂ y T y ∂ w ^ − ∂ ( y T X ) w ^ ∂ w ^ − ∂ w ^ T ( X T y ) ∂ w ^ + ∂ w ^ T ( X T X ) w ^ ∂ w ^ 根 据 矩 阵 的 微 分 公 式 : ∂ ( X T y ) T w ^ ∂ w ^ = ∂ w ^ T ( X T y ) ∂ w ^ = X T y ∂ w ^ T ( X T X ) w ^ ∂ w ^ = ( A + A T ) w ^ ∂ E w ^ ∂ w ^ = 0 − X T y − X T y − ( X T X + ( X T X ) T ) w ^ = 2 X T ( X w ^ − y ) 令 ∂ E w ^ ∂ w ^ = 0 逐 步 化 简 : 这 里 需 要 注 意 这 里 建 立 在 , X 不 是 奇 异 矩 阵 , 可 逆 . 2 X T X w ^ = 2 X T y X T X w ^ = X T y ( X T ) − 1 X T X w ^ = ( X T ) − 1 X T y X w ^ = ( X T ) − 1 X T y X − 1 X w ^ = X − 1 ( X T ) − 1 X T y w ^ = X − 1 ( X T ) − 1 X T y = ( X T X ) − 1 X T y w ^ ∗ = ( X T X ) − 1 X T y = X − 1 ( X T ) − 1 X T y = X − 1 y \frac{\partial E_{\hat{w}}}{\partial \hat{w}} = \frac{\partial y^Ty }{\partial \hat{w}} - \frac{\partial (y^TX)\hat{w} }{\partial \hat{w}} - \frac{\partial \hat{w}^T(X^Ty) }{\partial \hat{w}} + \frac{\partial \hat{w}^T(X^TX)\hat{w} }{\partial \hat{w}}\\
根据矩阵的微分公式:
\frac{\partial (X^Ty)^T\hat{w} }{\partial \hat{w}} = \frac{\partial \hat{w}^T(X^Ty) }{\partial \hat{w}} = X^Ty\\
\frac{\partial \hat{w}^T(X^TX)\hat{w} }{\partial \hat{w}} = (A + A^T)\hat{w}\\
\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 0 - X^Ty - X^Ty - (X^TX + (X^TX)^T)\hat{w} = 2X^T(X\hat{w} - y)\\
令\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 0\\
\\
逐步化简:\\
这里需要注意这里建立在, X不是奇异矩阵, 可逆.\\
2X^TX\hat{w} = 2 X^Ty\\
X^TX\hat{w} = X^Ty\\
(X^T)^{-1}X^TX\hat{w} = (X^T)^{-1}X^Ty\\
X\hat{w} = (X^T)^{-1}X^Ty\\
X^{-1}X\hat{w} = X^{-1}(X^T)^{-1}X^Ty\\
\hat{w} = X^{-1}(X^T)^{-1}X^Ty = (X^TX)^{-1}X^Ty\\
\\
\hat{w}^* = (X^TX)^{-1}X^Ty = X^{-1}(X^T)^{-1}X^Ty = X^{-1}y
∂ w ^ ∂ E w ^ = ∂ w ^ ∂ y T y − ∂ w ^ ∂ ( y T X ) w ^ − ∂ w ^ ∂ w ^ T ( X T y ) + ∂ w ^ ∂ w ^ T ( X T X ) w ^ 根 据 矩 阵 的 微 分 公 式 : ∂ w ^ ∂ ( X T y ) T w ^ = ∂ w ^ ∂ w ^ T ( X T y ) = X T y ∂ w ^ ∂ w ^ T ( X T X ) w ^ = ( A + A T ) w ^ ∂ w ^ ∂ E w ^ = 0 − X T y − X T y − ( X T X + ( X T X ) T ) w ^ = 2 X T ( X w ^ − y ) 令 ∂ w ^ ∂ E w ^ = 0 逐 步 化 简 : 这 里 需 要 注 意 这 里 建 立 在 , X 不 是 奇 异 矩 阵 , 可 逆 . 2 X T X w ^ = 2 X T y X T X w ^ = X T y ( X T ) − 1 X T X w ^ = ( X T ) − 1 X T y X w ^ = ( X T ) − 1 X T y X − 1 X w ^ = X − 1 ( X T ) − 1 X T y w ^ = X − 1 ( X T ) − 1 X T y = ( X T X ) − 1 X T y w ^ ∗ = ( X T X ) − 1 X T y = X − 1 ( X T ) − 1 X T y = X − 1 y
在PCA&SVD-摘要 | Lian (kyouichirou.github.io) , 已经讨论过为什么在实际的计算中, 并不会直接使用上述的normal equations来计算相关性系数, 而是采用svd的方式.
w ^ ∗ = ( X T X ) − 1 X T y X 的 逆 , X − 1 的 计 算 是 很 费 时 间 , 同 时 意 味 着 上 述 的 公 式 是 建 立 在 X 存 在 逆 的 前 提 的 基 础 之 上 的 . 将 上 述 公 式 转 换 为 s v d 形 式 : u , s , v = s v d ( X ) w ^ ∗ = v ( s 2 ) − 1 s ∗ u T ∗ y \hat{w}^* = (X^TX)^{-1}X^Ty\\
X的逆, X^{-1}的计算是很费时间, 同时意味着上述的公式是建立在X存在逆的前提的基础之上的.\\
将上述公式转换为svd形式:\\
u, s, v = svd(X)\\
\hat{w}^* = v(s ^ 2)^{-1} s*u^T * y\\
w ^ ∗ = ( X T X ) − 1 X T y X 的 逆 , X − 1 的 计 算 是 很 费 时 间 , 同 时 意 味 着 上 述 的 公 式 是 建 立 在 X 存 在 逆 的 前 提 的 基 础 之 上 的 . 将 上 述 公 式 转 换 为 s v d 形 式 : u , s , v = s v d ( X ) w ^ ∗ = v ( s 2 ) − 1 s ∗ u T ∗ y
import numpy as np
def svd_ols(A, b):
u, s, v = np.linalg.svd(A, full_matrices=False)
s = np.mat(np.diag(s))
v = np.mat(v)
u = np.mat(u)
return v.T * (s ** 2).I * s * u.T * b
y =np.array([
3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21
])
y = y[:, np.newaxis]
x = np.array([[e, 1] for e in range(1, 21)])
svd_ols(x, y)
matrix([[0.96992481],
[0.51578947]])
尽管svd解决了X的逆的问题, 但对于巨型数据, 速度还是不够快, 梯度下降这些使用模拟逼近最优(局部/全局)的方式因应而生, 详情见: 机器学习-梯度下降的简单理解 | Lian (kyouichirou.github.io)
九. SciPy稀疏矩阵
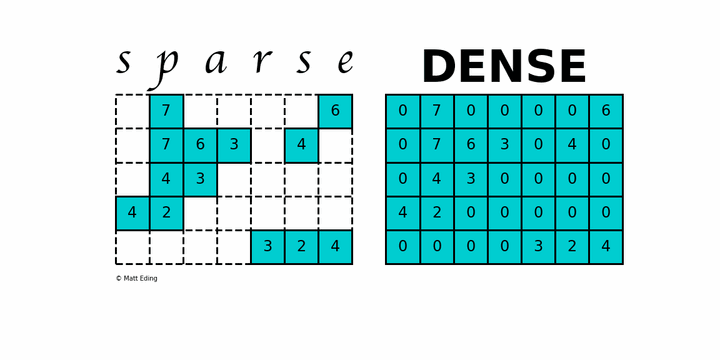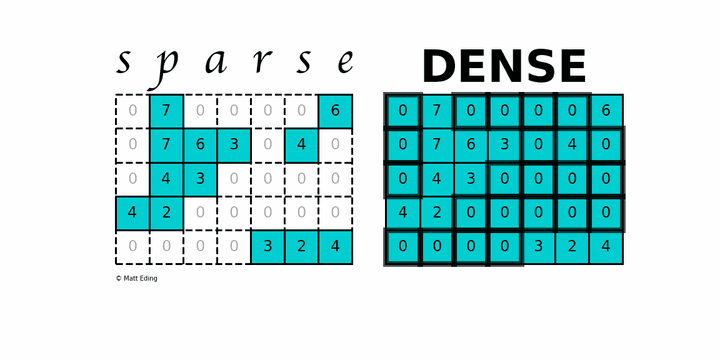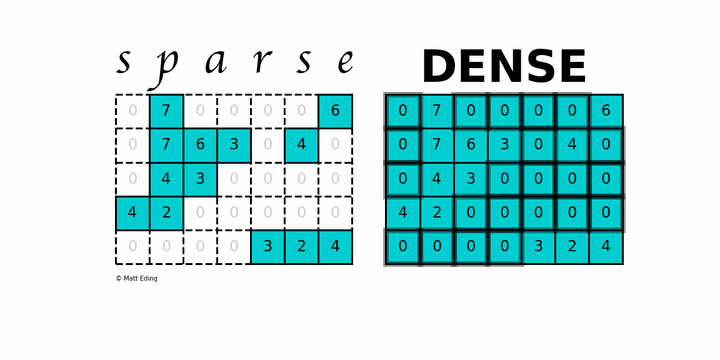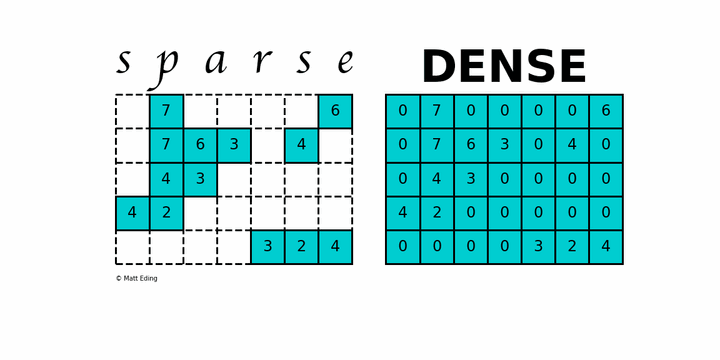
稀疏矩阵( sparse matrix ) 指的是绝大多数数值为零的矩阵. 反之 如果大部分元素都非零 则称为稠密矩阵( Dense ), 在实际的计算中, 稀疏矩阵是非常常见的, 由于大部分的内容为0, 即大量的内存空间被浪费.
from scipy import sparse
sparse?
'''
.. autosummary::
:toctree: generated/
bsr_matrix - Block Sparse Row matrix
coo_matrix - A sparse matrix in COOrdinate format
csc_matrix - Compressed Sparse Column matrix
csr_matrix - Compressed Sparse Row matrix
dia_matrix - Sparse matrix with DIAgonal storage
dok_matrix - Dictionary Of Keys based sparse matrix
lil_matrix - Row-based list of lists sparse matrix
spmatrix - Sparse matrix base class
'''
# 构造一个稀疏矩阵
# 行列坐标
row = [1, 3, 0, 2, 4]
col = [1, 4, 2, 3, 3]
# 每个坐标存储的元素
data = [2, 5, 9, 1, 6]
m = sparse.coo_matrix((data, (row, col)), shape=(6, 7))
m.data
array([2, 5, 9, 1, 6])
m.toarray()
array([[0, 0, 9, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 5, 0, 0],
[0, 0, 0, 6, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])
mdata = m.toarray()
# 压缩
n = sparse.csr_matrix(mdata)
n.data
array([9, 2, 1, 5, 6], dtype=int32)
print(n)
(0, 2) 9
(1, 1) 2
(2, 3) 1
(3, 4) 5
(4, 3) 6
n.toarray()
array([[0, 0, 9, 0, 0, 0, 0],
[0, 2, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 5, 0, 0],
[0, 0, 0, 6, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]], dtype=int32)
十. numpy-linalg(线性代数)
numpy, python科学计算基石之一.
10.1 矩阵和向量积
方法
描述
doto (a, b[, out])两个数组的点积.
linalg (arrays)在单个函数调用中计算两个或更多数组的点积 同时自动选择最快的求值顺序.
vdot (a, b)返回两个向量的点积.
inner (a, b)两个数组的内积.
outer (a, b[, out])计算两个向量的外积.
matmul (x1, x2, /[, out, casting, order, …])两个数组的矩阵乘积.
tensordot (a, b[, axes])沿指定轴计算张量点积.
einsum (subscripts, *operands[, out, dtype, …])计算操作数上的爱因斯坦求和约定.
einsum_path (subscripts, *operands[, optimize])通过考虑中间数组的创建 计算einsum表达式的最低成本压缩顺序.
linalg.matrix_power (a, n)将方阵提升为(整数)n次方.
kron (a, b)两个数组的Kronecker乘积.
10.2 分解
10.3 矩阵特征值
10.4 范数和其他数字
方法
描述
linalg.norm (x[, ord, axis, keepdims])矩阵或向量范数.
linalg.cond (x[, p])计算矩阵的条件数.
linalg.det (a)计算数组的行列式.
linalg.matrix_rank (M[, tol, hermitian])使用SVD方法返回数组的矩阵的rank
linalg.slogdet (a)计算数组行列式的符号和( 自然) 对数.
trace (a[, offset, axis1, axis2, dtype, out])返回数组对角线的和.
10.5 解方程和逆矩阵
10.6 异常
十一. 参考
< 机器学习实战: 基于Scikit-Learn Keras和TensorFlow 第二版 >, 奥雷利安- 杰龙
< 矩阵分析与应用 第二版>, 张贤达
非常好的工具书.