Lian
文章目录 站点概览

Lian

make thing better and simpler.

95 文章
64 标签

报童问题(Newsvendor Problem)详解

发布于 2023-04-07 | 标签: operational research 、 matlab 、 math model 、 sympy 、 scipy 、 business 、 statistics 、 python | 38分钟 | 8273字数
ppRGBBd.jpg

Buying a newspaper. The spirit of the Ghetto.1902 - Newsvendor model - Wikipedia

一. 前言

1.1 泊松分布

即 poisson distribution, 离散概率分布, 适合于描述单位时间内随机事件发生的次数.

P(X=k)=e−λλkk!泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率.泊松分布适合于描述单位时间内随机事件发生的次数.如某一服务设施在一定时间内到达的人数电话交换机接到呼叫的次数汽车站台的候客人数机器出现的故障数自然灾害发生的次数等等.若随机变量X取0和一切正整数值在n次独立试验中出现的次数x恰为k次的概率P(X=k)=(k=0,1,...,n)式中λ是一个大于0的参数此概率分布称为泊松分布.它的期望值为E(x)=λ方差为D(x)=λ.当n很大且在一次试验中出现的概率P很小时泊松分布近似二项分布.P(X = k) = \frac{e ^ {-\lambda}\lambda^k}{k!}\\ \\ 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率. \\ \\ 泊松分布适合于描述单位时间内随机事件发生的次数. \\ 如某一服务设施在一定时间内到达的人数 电话交换机接到呼叫的次数 \\ 汽车站台的候客人数 机器出现的故障数 自然灾害发生的次数等等. \\ \\ 若随机变量X取0和一切正整数值 在n次独立试验中出现的次数x恰为k次的概率\\ P( X=k) =( k=0,1,...,n) \\ 式中λ是一个大于0的参数 此概率分布称为泊松分布. \\ 它的期望值为E(x)=λ 方差为D(x) = λ. \\ 当n很大 且在一次试验中出现的概率P很小时 泊松分布近似二项分布.

泊松分布, 一般需满足以下四个条件:

  • 给定区域内的特定事件产生的次数 可以是根据时间 长度 面积来定义;
  • 各段相等区域内的特定事件产生的概率是一样的;
  • 各区域内 事件发生的概率是相互独立的;
  • 当给定区域变得非常小时 两次以上事件发生的概率趋向于0.

1.2 二项分布

1.2.1 伯努利分布

亦或者成为0 - 1 分布

P(x)=px(1−p)1−x={pif  x=1qif  x=0q=1−pP(x) = p ^ x (1 - p) ^ {1-x} = \left\{\begin{aligned}p\quad if \; x = 1 \\ q \quad if \; x = 0\end{aligned}\right.\\ \\ q = 1 - p

二项分布是n个独立的成功/失败试验中成功的次数的离散概率分布, 二项分布 其中每次试验的成功概率为p. 这种单次成功/失败试验被称为伯努利试验 而当n = 1时 二项分布就是伯努利分布.

P(x)=Cnxpx(1−p)n−x=n!x!(n−x)!px(1−p)n−x记作:X∼B(n,  p)二项分布的期望为:E(X)=npX的方差为:D(X)=np(1−p)这个事实很容易证明.首先假设有一个伯努利试验.试验有两个可能的结果:1和0前者发生的概率为p后者的概率为1−p.该试验的期望值等于μ=1 − p+0 − (1−p)=p.该试验的方差也可以类似地计算:σ2=(1−p)2−p+(0−p)2−(1−p)=p(1 − p).一般的二项分布是n次独立的伯努利试验的和.它的期望值和方差分别等于每次单独试验的期望值和方差的和:P(x) = C^x_np^x(1-p)^{n-x} = \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}\\ \\ 记作: X\sim B(n,\; p)\\ 二项分布的期望为:\\ E(X) = np\\ X的方差为:\\ D(X) = np(1 - p)\\ 这个事实很容易证明. 首先假设有一个伯努利试验. \\ 试验有两个可能的结果: 1和0 前者发生的概率为p 后者的概率为1−p. \\ 该试验的期望值等于μ= 1 -  p+ 0 -  (1−p) =p. \\ 该试验的方差也可以类似地计算: σ2= (1−p)2- p+ (0−p)2- (1−p) =p(1 − p).\\ 一般的二项分布是n次独立的伯努利试验的和. 它的期望值和方差分别等于每次单独试验的期望值和方差的和:\\ \\

当 n 足够大的时候, 正态分布对于离散型二项分布能够很好地近似.

1.3 正态分布

若随机变量X服从一个数学期望为μ方差为σ2的正态分布记为N(μσ2).其概率密度函数为正态分布的期望值μ决定了其位置其标准差σ决定了分布的幅度.当μ=0,σ=1时的正态分布是标准正态分布.f(x)=1σ2πe−12(x−μσ)2记作X∼N(μ,σ2)σ,为标准偏差(standard−deviation)μ,均值(mean),期望(expectation)σ(基于样本)=∑(x−xˉ)(n−1)若随机变量X服从一个数学期望为μ 方差为\sigma^2的正态分布 记为N(μ σ2). \\ 其概率密度函数为正态分布的期望值μ决定了其位置 其标准差σ决定了分布的幅度. \\ 当μ = 0,σ = 1时的正态分布是标准正态分布. \\ \\ f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{-1}{2}(\frac{x - \mu}{\sigma})^2}\\ \\ 记作 X \sim N(\mu, \sigma ^ 2)\\ \sigma, 为标准偏差(standard-deviation)\\ \mu, 均值(mean), 期望(expectation)\\ \\ \sigma(基于样本) = \sqrt{\frac{\sum(x - \bar x)}{(n- 1)}}

标准正态分布, 即

当μ=0,σ=1时,正态分布就成为标准正态分布f(x)=12πe(−x22)当 \mu = 0, \sigma = 1时, 正态分布就成为标准正态分布 \\ f(x) = \frac{1}{\sqrt{2\pi}}e^{(-\frac{x^2}{2})}

1.4 正态与泊松

img

先要介绍一个重要的公式: 斯特林公式_百度百科 (baidu.com)

n!≈2πn(ne)nlim⁡n→+∞n!2πn(ne)n=1lim⁡n→∞π(λ)=N(μ,σ2)π(n;λ)=λne−λn!=λne−λ2πn(n+1/2)e−n=λλ(1+δ)e−λ2π[λ(1+δ)](λ(1+δ)+1/2)e−λ(1+δ)π(n;λ)=λλ(1+δ)e−λ2π[λ(1+δ)]λ(1+δ)+1/2e−λ(1+δ)=eλδ(1+δ)−λ(1+δ)−1/22πλ=e−λδ2/22πλn! \approx \sqrt{2\pi n}(\frac{n}{e})^n\\ \lim_{n\rightarrow+\infty} \frac{n!}{ \sqrt{2\pi n}(\frac{n}{e})^n} = 1\\ \lim _{n \rightarrow \infty} \pi(\lambda)=\mathbb{N}\left(\mu, \sigma^{2}\right) \\ \\ \begin{aligned} \pi(n ; \lambda)&=\frac{\lambda^{n} e^{-\lambda}}{n !}\\ &=\frac{\lambda^{n} e^{-\lambda}}{ \sqrt{2 \pi} n^{(n+1 / 2)} e^{-n}}\\ &=\frac{\lambda^{\lambda(1+\delta)} e^{-\lambda}}{ \sqrt{2 \pi} [{\lambda(1+\delta)}]^{({\lambda(1+\delta)}+1 / 2)} e^{-{\lambda(1+\delta)}}}\\ \end{aligned}\\ \begin{aligned} \pi(n ; \lambda)&=\frac{\lambda^{\lambda(1+\delta)} e^{-\lambda}}{\sqrt{2 \pi} [\lambda(1+\delta)]^{\lambda(1+\delta)+1 / 2}e^{-\lambda(1+\delta)}} \\ &=\frac{e^{\lambda \delta}(1+\delta)^{-\lambda(1+\delta)-1 / 2}}{\sqrt{2 \pi \lambda}} \\ &=\frac{e^{-\lambda \delta^{2} / 2}}{\sqrt{2 \pi \lambda}} \end{aligned}

二. 报童问题

报童问题, 即newsvendor problem, 亦或者 Newsvendor Model.

The classic newsvendor problem Arrow, Harris, and Marschak (1951) describes a decision-maker who must decide upon an order quantity in each ordering period, given an unknown demand from a known distribution, such that the risk of over-ordering and under-ordering are balanced. Over the past decades, the field of operations management has seen numerous studies testing analytical models related to inventory management and decision-making under risk in laboratory experiments only to discover the lack of " rationality" in the human decision-making processes. However, behavioral studies on the newsvendor problem show that participants in a relatively simple decision-making scenario significantly deviated from the decisions that optimized profits.

  • 订货数量(每个特定区间周期).
  • 不确定需求.
  • 已知的分布(历史数据反推).
  • 库存管理.
  • 报童问题是多种需求(库存)问题的简化模式.
ppm8oRg.png

简而言之, 商人一天(每天)应该订购多少报纸才能实现预期效益(E)最大化的问题? 更简单就是, 报纸定多了卖不完, 定少了不够买.

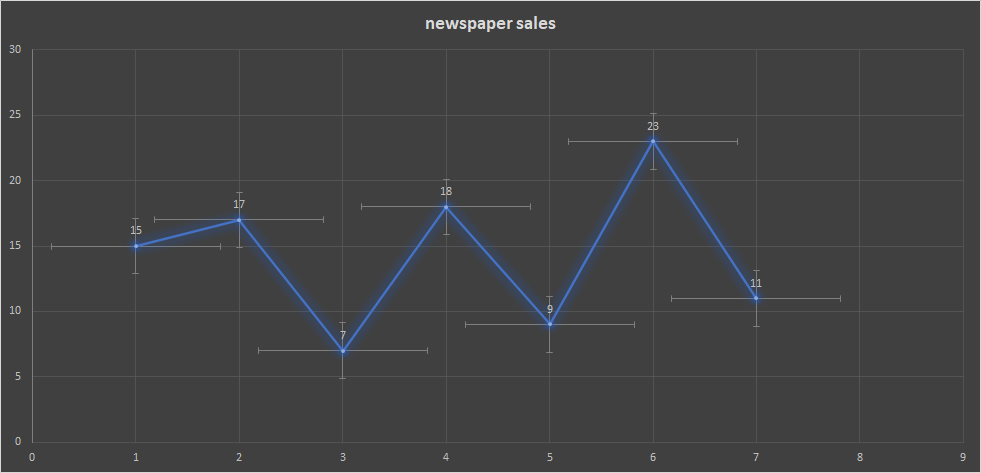
假设存在历史销售数据(如企业历史积累的数据), 其中的部分, 每天销售的报纸数量如下, 每7天一个周期

date quantities
1 15
2 17
3 7
4 18
5 9
6 23
7 11
pp7S5fH.png

报纸7天内的平均日销量为:xˉ=avg(sum(quanlities))=14.285714285714286报纸7天内的平均日销量为: \\ \bar x = avg(sum(quanlities)) = 14.285714285714286

2.1 模型构建

参数解析:

报纸的订购每份价格 c: 0.5

报纸的零售每份价格 q: 1

报纸的每份残值 s: 0.05 (当废纸处理)

其中 q > c >> s

每天销量为: x

每天订购的数量为: d

可得到以下函数:g(d)=x∗q−d∗c+(d−x)∗sa情形:  供不应求(或者刚好平衡),  g(d)=(q−c)∗db情形:  供不大于求,  g(d)=x∗q−d∗c+(d−x)∗s其中每日的销量x满足特定的随机分布,这里假设x为连续型变量f(x)∼x将上述的式子进行变换:g(d)=∑x=0d(x∗q−d∗c+(d−x)∗s)∗f(x)+∑x=d+1∞(q−c)∗d∗f(x)转换为密度函数的形式:f(x),x=(1,2,3,...)转换为∫p(x)dxg(d)=∫0d(x∗q−d∗c+(d−x)∗s)∗p(x)dx+∫x=d∞(q−c)∗d∗p(x)dx可得到以下函数:\\ g(d) = x * q - d * c + (d - x) * s\\ a情形:\;供不应求(或者刚好平衡), \; g(d) = (q - c) * d\\ b情形:\;供不大于求, \; g(d) = x * q - d * c + (d - x) * s\\ \\ 其中每日的销量x满足特定的随机分布, 这里假设x为连续型变量\\ f(x) \sim x\\ 将上述的式子进行变换:\\ g(d) = \sum_{x=0}^{d}(x * q - d * c + (d - x) * s) * f(x) + \sum_{x=d+1}^\infty(q - c) * d * f(x)\\ 转换为密度函数的形式:\\ f(x), x = (1,2,3,...) 转换为 \int p(x)\mathrm{d}x\\ g(d) = \int_0^d (x * q - d * c + (d - x) * s)*p(x) dx + \int_{x=d}^\infty(q - c) * d*p(x)\mathrm{d}x

即, 使得函数g(d)的取值达到最大值.

2.2 问题简化

在实际的业务场景很多时候, 缺货是需要优先考虑的, 特别是在业务高度成熟之后, 因为对于类似于Amazon等电商平台, 热销的产品缺货将可能会导致很多问题, 如搜索权重被大幅度调低(这种变化很多时候补货后也难以挽回).

隐含额外目标: 保证供应充足, 宁愿超出一定数量, 也不希望出现缺货的情形.

即, 模型需要实现两个主要目标:

  • 收益最大化
  • 最大程度满足市场需求

故而,可以先将问题局限在, 商人需要每天备多少的报纸才能满足市场的需求, 在这个基础上对订购数量进行调整.

以下仅仅是演示, 假设数据满足的分布, 并不说上述假设数据满足以下的分布.

2.2.1 离散型

假设商人每天的销售时间段为:07:00−12:00⎵将每份报纸销售拆成若干时间段内发生的事情:07:00−08:00⎵−08:00−09:00⎵−09:00−10:00⎵−10:00−11:00⎵−11:00−12:00⎵即每个时间段t内,发生销售行为为:  卖出(1),  每卖出(0)由于时间段细分还是不够容纳所有的数据,假设拆分成为30个时间段则,假设在整个时间段T内卖出5份报纸的概率为P(x=5)=C305p5(1−p)25将时间T拆分为n份,n趋向于→∞P(x)=Cn5p5(1−p)n−5即T时间段内的销售出去k个报纸的概率为:P(x)=lim⁡n→+∞Cnkpk(1−p)n−k可以看到,当前问题被转为二项分布问题,即进行n次的伯努利试验,每次都是卖出(1),不卖出(0)从上面的二项分布可知E(X)=np=μp=μn将p代入上述的极限中:P(x)=lim⁡n→+∞Cnk(μn)k(1−μn)n−k化简:P(x)=lim⁡n→+∞Cnk(μn)k(1−μn)n−k=μkk!e−μ即泊松分布的概率分布函数:P(X=k)=e−λλkk!μ=λ假设商人每天的销售时间段为: \\ \underbrace{07:00 - 12:00}\\ \\ 将每份报纸销售拆成若干时间段内发生的事情: \\ \underbrace{07:00 - 08:00}-\underbrace{08:00 - 09:00}-\underbrace{09:00 - 10:00}-\underbrace{10:00 - 11:00}-\underbrace{11:00 - 12:00}\\ 即每个时间段t内, 发生销售行为为:\;卖出(1),\;每卖出(0) \\ 由于时间段细分还是不够容纳所有的数据, 假设拆分成为30个时间段\\ 则, 假设在整个时间段T内卖出5份报纸的概率为\\ P(x=5) = C^{5}_{30}p^5(1-p)^{25}\\ 将时间T拆分为n份, n趋向于\rightarrow\infty\\ P(x) = C^5_np^5(1-p)^{n-5}\\ 即T时间段内的销售出去k个报纸的概率为:\\ P(x) = \lim_{n\rightarrow+\infty}C^k_np^k(1-p)^{n - k}\\ \\ 可以看到, 当前问题被转为二项分布问题, 即进行n次的伯努利试验, 每次都是卖出(1), 不卖出(0) \\ 从上面的二项分布可知 E(X) = np = \mu\\ p = \frac{\mu}{n}\\ \\ 将p代入上述的极限中:\\ P(x) = \lim_{n\rightarrow+\infty}C^k_n(\frac{\mu}{n})^k(1-\frac{\mu}{n})^{n - k}\\ 化简:\\ P(x) = \lim_{n\rightarrow+\infty}C^k_n(\frac{\mu}{n})^k(1-\frac{\mu}{n})^{n - k} = \frac{\mu^k}{k!}e^{-\mu}\\ 即泊松分布的概率分布函数: P(X = k) = \frac{e ^ {-\lambda}\lambda^k}{k!}\\ \mu = \lambda\\

得到上述内容后, 计算

xˉ=14.3≈μ可计算:P(X=k)=e−1014.3kk!k=(0,1,2,3....)\bar x = 14.3 \approx \mu\\ 可计算:\\ P(X = k) = \frac{e ^ {-10}14.3^k}{k!}\\ k = (0, 1, 2, 3....) 

import math
import plotly.graph_objects as go
from plotly.subplots import make_subplots
import pandas as pd

sales = [
    15,
    17,
    7,
    18,
    9,
    23,
    11
]
avg = sum(sales) /len(sales) # 14.285714285714286

# 泊松分布概率分布函数
ps = lambda k: (math.e ** (- avg) * avg ** k) / math.factorial(k)

data = [ps(i) for i in range(1, 30)]

df = pd.DataFrame()
df['quantities'] = range(1, 30)
df['probability'] = data
df.head(3)
quantities probability
1 0.000009
2 0.000064
3 0.000304 
# 帕累托累加
df['cum'] = df['probability'].cumsum()
df.head()
  quantities  probability	cum
0	1	0.000009	0.000009
1	2	0.000064	0.000073
2	3	0.000304	0.000376
3	4	0.001084	0.001461
4	5	0.003098	0.004559

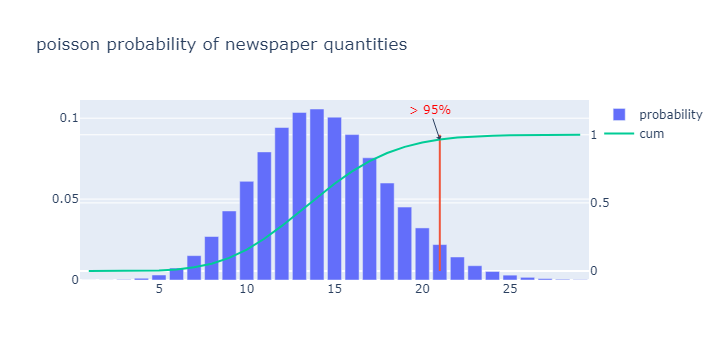
# 在quantities = 21时, 满足市场需求的可能性大于0.95
q = df.loc[df['cum'] > 0.95].iloc[0, 0]
21

# 等价于
from scipy.stats import poisson

ls = poisson(avg)
tmp = [ls.cdf(i) for i in range(1, 30)]

# 返回累积概率1-21
ls.cdf(21)
0.9653094499403743

# 多轴方式不要使用官方文档的示例, 会导致绘制第二轴时, 出现问题, 在增加注释和垂直的线时

# 概率分布
trace1 = go.Bar(
    x=df['quantities'],
    y=df['probability'],
    name='probability'
)

# 显示q的垂直线
trace2 = go.Scatter(
    x= [q] * 29,
    y = df['cum'],
    name=str(q),
    showlegend=False,
    xaxis='x',
    yaxis='y2'
)

# 累积曲线
trace3 = go.Scatter(
    x =df['quantities'],
    y = df['cum'],
    name='cum',
    xaxis='x',
    yaxis='y2'
)

data = [trace1, trace2, trace3]
layout = go.Layout(
    # 设置坐标轴的格式 一般次坐标轴在右侧
    yaxis2=dict(
        anchor='x',
        overlaying='y',
        side='right'
    )
)

fig = go.Figure(data=data, layout=layout)

fig.add_annotation(
    x=q,
    y=df.loc[df['cum'] > 0.95].iloc[0, 2],
    text="> 95%",
    # 设置以第二轴来添加注释
    yref="y2",
    # 颜色
    font_color='red',
    # 显示注释箭头
    showarrow=True,
    secondary_y=True,
    # 设置为箭头
    arrowhead=1
)

fig.update_layout(
    width=720,
    height=360,
    title='probability of newspaper quantities'
)
fig.show()
pp7ShkD.png

(plotly绘制的是动态可交互的图, 不是静态图)

即, d 的取值在21时, 已经有95%的可能性是满足市场的需求的.

2.2.2 连续型

离散型随机变量

即, discrete random variable, 如果随机变量 X 的所有值都可以逐个列举出来, 则称 X 为离散型随机变量.

连续型随机变量

即, continuous random variable, 如果随机变量 X 的所有值不可以逐个列举出来, 则称 X 为连续型随机变量.

假设, 该问题的销量概率密度函数 f(x) 服从正态分布.

g(d)=∑x=0n(x∗q−d∗c+(d−x)∗s)∗f(x)+∑x=d+1∞(q−c)∗d∗f(x)g(d) = \sum_{x=0}^{n}(x * q - d * c + (d - x) * s) * f(x) + \sum_{x=d+1}^\infty(q - c) * d * f(x) 

from scipy import stats

stats.tstd(sales)
# 5.618845839799182

# 这里需要注意在计算的时候stats.tstd() 
# 在这里关于Excel图表中误差线的计算问题所讨论的问题
# STDEV.S, STDEV.P, 即样本偏差还是整体的偏差
# 亦或者, 无偏估计, 有偏估计

np.std(sales)
5.202040416009464, 注意numpy提供的计算, 默认状态, 计算的方式 = STDEV.P

# 需要手动指定
np.std(sales, ddof=1) # 和下面的stats反向操作
5.618845839799182

ddofint, optional
Means Delta Degrees of Freedom. 
The divisor used in calculations is N - ddof, where N represents the number of elements. 
By default ddof is zero.

# Delta degrees of freedom. Default is 1.
stats.tstd(sales, ddof=0)
5.202040416009464

# 这种计算上的差异, 在其他的api上也同样如此
# 例如方差的计算

从前面已经知道μ=14.3σ=5.6从前面已经知道\\ \mu = 14.3\\ \sigma = 5.6 

x = np.arange(avg - 4 * std, avg + 4 * std, 0.01)
y = stats.norm.pdf(x, avg, std)

px.line(
    x = x,
    y= y,
    width=720,
    height=480,
    title='probability of newspaper quantities'
)
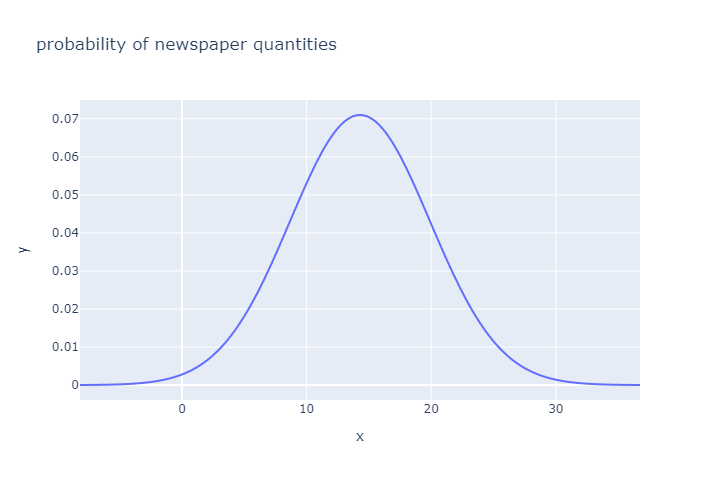
pp7S4te.png
stats.norm.ppf(0.95, avg, std)

# 23.52789324458916

即订货 d 的取值在24时, 满足市场需求的概率超过95%.

f(x)=p(x)dxg(d)=∫0d(x∗q−d∗c+(d−x)∗s)∗p(x)dx+∫d∞(q−c)∗d∗p(x)dx由于数据在35左右,  p(35)≈0即P(x<35)=1f(x) = p(x)\mathrm{d}x\\ g(d) = \int_0^d (x * q - d * c + (d - x) * s)*p(x) dx + \int_{d}^\infty(q - c) * d*p(x)\mathrm{d}x\\ 由于数据在35左右, \; p(35) \approx 0\\ 即P(x < 35) = 1

代入前面模型中预设的数值计算:

g(d)=∫0d(x∗1−d∗0.5+(d−x)∗0.05)∗p(x)dx  +∫d∞0.5∗d∗p(x)dxg(d)=∫0d(0.95x−0.45d)∗p(x)dx  +∫d∞0.5d∗p(x)dxg(d) = \int_0^d (x * 1 - d * 0.5 + (d - x) * 0.05)*p(x) dx \;+ \int_{d}^\infty0.5 * d*p(x)\mathrm{d}x\\ g(d) = \int_0^d (0.95x - 0.45d)*p(x) dx \;+ \int_{d}^\infty0.5d*p(x)\mathrm{d}x\\

关于积分计算的方式, 注意sympy在这里计算会出现的一些问题.

注意: 这里的代码和其他内容无关, 仅作为备忘

from sympy import integrate,  Symbol
from sympy.stats import Normal, density
import math
import numpy as np
from scipy.stats import norm

X = Normal("x", 10, 2.5)
x = Symbol('x')

## 获得正态分布的概率密度函数
ts = density(X)(x)
ts

0.22e−0.08(x−102)π\frac{0.2\sqrt{2e}^{-0.08(x-10^2)}}{\sqrt{\pi}} 

integrate(density(X)(x), (x, 0, 1))

9.0111813176641⋅10−52这个值是:F(1)=∫01f(x)dx不是norm.pdf的值9.0111813176641⋅10^{-5}\sqrt{2}\\ 这个值是:\\ F(1) = \int_{0}^1f(x)\mathrm{d}x\\ 不是norm.pdf的值\\ 

# 默认状态下不会自动转为浮点数
integrate(density(X)(x), (x, 0, 1)).evalf()

# 0.000127437348324436

9.0111813176641 * math.pow(10, -5) * math.sqrt(2)

# 0.0001274373483244363

integrate(density(X)(x), (x, -np.inf, 1))
## 等价于
norm.cdf(1, 10, 2.5)

# 0.0001591085901575871
# 逆cdf函数
norm.ppf(0.0001591085901575871, 10, 2.5)
# 1.0000000000002185

F(1)=∫−∞1f(x)dxF(1) = \int_{-\infty}^1f(x)\mathrm{d}x\\ 

# 注意区分开离散型和连续型分布的差异
# 这里得到的概率可能性只是概念上的, 并不是和离散型的一样是具体的指向, 某个点-概率这种关系
# 可以认为是参考指标

norm.pdf(1, 10, 2.5)
# 0.00024476077204550875

# 等价于, 直接输入公式来计算
(0.2 * math.sqrt(2) * \
math.pow(math.e, -8.0 *(0.1 - 1) ** 2))/math.sqrt(math.pi)

这里计算g(d)函数的积分时出现问题, 而且很慢, 这里使用scipy的integrate来计算上述的函数积分.

The scipy.integrate sub-package provides several integration techniques including an ordinary differential equation integrator. An overview of the module is provided by the help command:

from scipy import integrate

def part_one(x, d):
    return (0.95 * x - 0.45 * d) * stats.norm.pdf(x, avg, std)

def part_tow(x, d):
    return 0.5 * d * stats.norm.pdf(x, avg, std)

# 在上面部分已经提及当数据在35左右已经趋近于0, 所以这里的无穷可以直接使用35替代即可
rs = []
for i in range(1, 35):
    # quad返回两个值, 一个是计算结果, 一个是误差
    # scipy速度非常快
    # sympy运行很慢, 对于复杂的函数
    rs.append(
        integrate.quad(test, 0, i, args=(i, ))[0] +\
            integrate.quad(part, i, 35, args=(i, ))[0] )

import plotly.express as px

px.line(
    x=range(1, 35),
    y=rs,
    text=["(" + str(i + 1) + ',' + str(round(e, 2)) + ")" for i, e in enumerate(rs) ],
    title='max profit',
    width=900,
    height=480
)
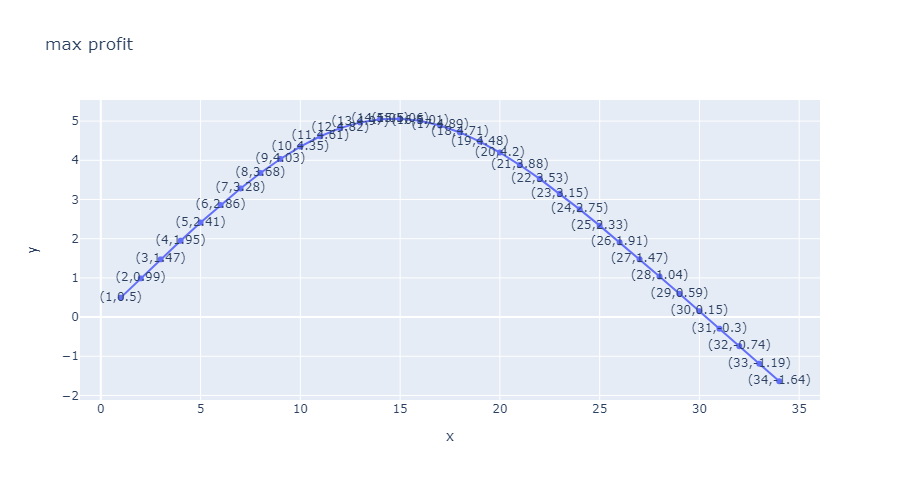
pp7Sopd.png

以上述模型假设的数值计算结果:

  • 最优解出现在15
  • 最大的获益可能为5.06
# 使用 matlab 来完成
# m的代码风格, JavaScript, vba, mysql的整合

clear;
clc;
mx = 35;
avg = 14.285714285714286;
sig = 5.618845839799182;

x = 0:1:mx;

part_a = @(x, d)(0.95 .* x - 0.45 .* d).* normpdf(x, avg,sig);
part_b = @(x, d)0.5 * d * normpdf(x, avg, sig);

# 声明0填充的数组, 相当于声明一个空数组
results = zeros(mx - 1, 1);

for d = 1:1:mx - 1
    results(d) = integral(@(x)part_a(x, d), 0, d) + integral(@(x)part_b(x, d), d, mx);
end

[m_profix, d_point] = max(results);
# 5.6188, 15

plot(1:1:mx-1, results);

xlabel('d');
ylabel('profit');
title('max profit of newpapers');
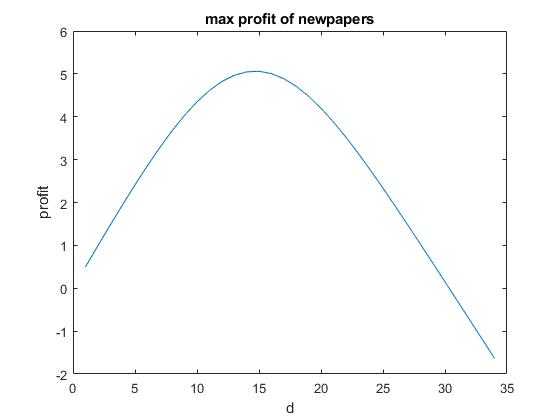
ppOLmxs.png

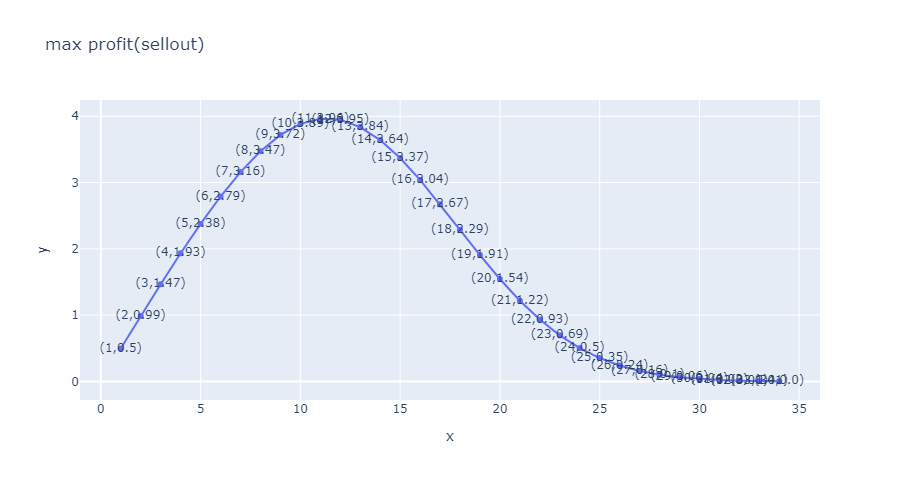
只考虑售罄情况, 最大值出现在11, 最大值为3.96

pp7S76I.png

只考虑无法完全出售的情况

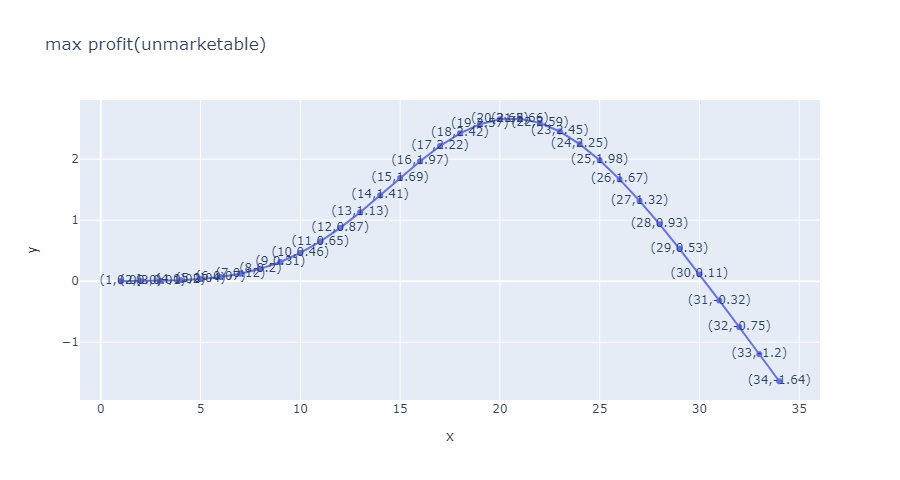
pp7ST1A.png

最大值出现在21, 最大利润2.66.

2.2.3 小结

回到最初的方程:

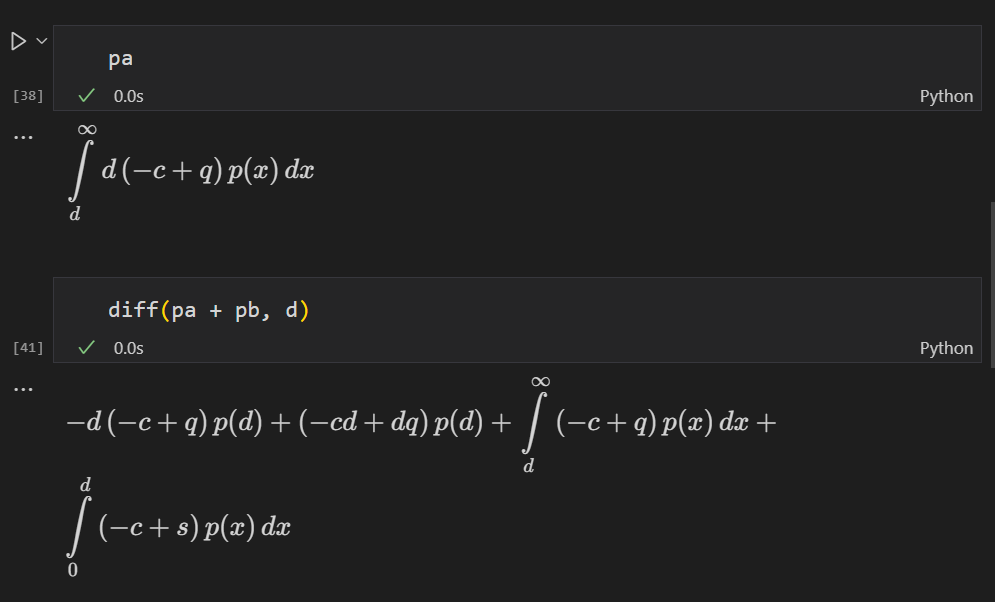
ppRtYhq.png
# 利用sympy创建出函数方程
# 但是需要注意sympy只能给出答案, 并不会化简, 需要手动化简

p = Function('p')

x, d, c, s, q= symbols('x d c s q')

pa = Integral((x * q - d * c + (d -x) * s) * p(x), (x, 0, d))
pb = Integral((q - c) *d* p(x), (x, d, +oo))

# 对d进行求导
diff(pa + pb, d)

# 求二阶导
diff(diff(pa + pb, d), d)
# diff(pa + pb, d, d), 多阶求导, 只需要在后面加上求导的参数即可
# 得到的二阶导数
# g''(d) >= 0, 函数g(d)为上凸函数

解得:

求导dgdd=0(根据凸函数特性,极值点为极大值)=∫d∞(−c+q)p(x)dx+∫0d(−c+s)p(x)dx(−c+q),(−c+s)均为常数,提取出来,化简得:∫0d  p(x)  dx∫d∞  p(x)  dx=q−cc−sP1=∫0d  p(x)  dx,表示的是没有完全售出,需求小于订货的概率分布密度累积.P2=∫d∞  p(x)  dx,表示需求大于等于订货,供不应求的情况的概率分布密度累积.由于,∫0∞p(x)  dx≈1即,F(d)=P(x≤d)=∫0dp(x)  dx=q−cq−s这里假设s远小于q,即F(d)=q−cq即,F(d)就转为了常见的数据统计指标,(产品)毛利率(gross  profit  margin),  gpm=q−cq∗100%P1P2,转换一下:r=q−cc−s当残值特别小的时候,r=q−cc=qc−1求导\frac{\mathrm{d}g}{\mathrm{d}d} = 0(根据凸函数特性, 极值点为极大值) = \int_d^\infty (-c + q)p(x)\mathrm{d}x + \int_0^d(-c + s)p(x)\mathrm{d}x\\ \\ (-c+q), (-c + s)均为常数, 提取出来, 化简得:\\ \\ \frac{\int_0^d\;p(x)\;\mathrm{d}x}{\int_d^{\infty}\;p(x)\;\mathrm{d}x} = \frac{q -c}{c -s}\\ P_1 = \int_0^d\;p(x)\;\mathrm{d}x, 表示的是没有完全售出, 需求小于订货的概率分布密度累积.\\ P_2 = \int_d^{\infty}\;p(x)\;\mathrm{d}x, 表示需求大于等于订货, 供不应求的情况的概率分布密度累积.\\ 由于,\quad \int_0^{\infty} p(x)\;\mathrm{d}x \approx 1\\ 即, F(d) = P(x \leq d) = \int_0^d p(x) \; \mathrm{d}x = \frac{q - c}{q - s} \\ 这里假设s远小于q, 即F(d) = \frac{q - c}{q}\\ 即, F(d)就转为了常见的数据统计指标, (产品)毛利率(gross\;profit\;margin),\; gpm = \frac{q - c}{q} * 100\%\\ \\ \frac{P_1}{P_2}, 转换一下: \\ r = \frac{q -c}{c -s}\\ \\ 当残值特别小的时候, r = \frac{q -c}{c} = \frac{q}{c} - 1 

# 将数据代入, 最佳的订货数量
F(d) = P = 0.5/0.95

d = stats.norm.ppf(P, avg, std)

# 14.656624483059883, => 15

由于残值在实际中是相对固定的, 波动的主要源自销售价格( q )和成本价格( c ), q / c 的比值越大, 订货策略可以趋于激进, 反之则相反.

同时, 对 F(d) 的最优求解, 实现了模型和实际数据指标之间的联系.

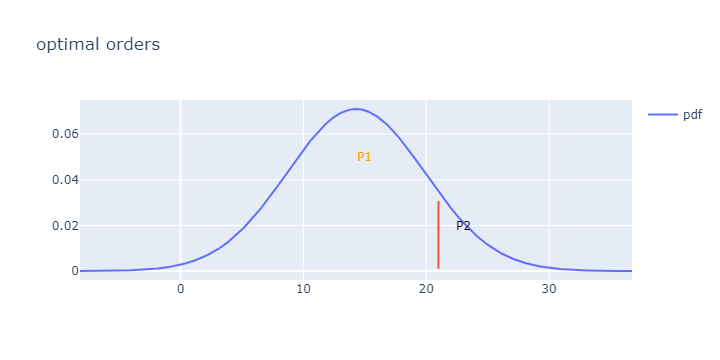
pp7pajI.png

(P1, P2)

trace2 = go.Scatter(
    x= x,
    y = y,
    name="pdf"
)

trace3 = go.Scatter(
    x = [21] * 10,
    y = [stats.norm.pdf(i, avg, std) for i in range(-2, 21)],
    mode='lines',
    name='gap',
    showlegend=False
)

data = [trace2, trace3]

fig = go.Figure(data=data)

fig.add_annotation(
    x=15,
    y=0.05,
    text="P1",
    showarrow=False,
    font_color='orange',
)

fig.add_annotation(
    x=23,
    y=0.02,
    text="P2",
    showarrow=False,
    font_color='black',
)

fig.update_layout(
    width=720,
    height=360,
    title='optimal orders'
)
fig.show()

2.3 扩展

  • 增加缺货的惩罚机制(损失), l
  • 仓储空间(假设报纸需要中转), i
  • 仓储成本(运输成本), ic
  • 采购成本和采购量的动态变化, 例如采购20份为0.5元, 采购10份0.6元, 即采购成本转为为特定的函数 C(d).

加入上述内容, 扩展模型, 但是需要注意, 模型是否还适合处理上述的问题.

三. 总结

上述对于历史销售数据的分布假设仅作为演示的示例, 实际的可能出现的分布形式还有很多.

报童模型, 是相对理想的状态, 现实中, 实际远比模型复杂, 需要考虑的变量也更多, 模型不宜生搬硬套.

  • 仓库仓储数量是有限的, 尽管销售情况很好, 但是限于仓库的存储能力.
  • 产品的生命周期是有限的, 特别是对于快消品而言(如季节性产品), 不能单纯从过往的数据来考虑问题.
  • 商人宁愿承受的风险程度, 和投资一样, 不同的风险对应的收益是不尽相同的, 通常而言, 高风险对应高收益, 低风险则反之.
  • 商人宁愿承受商品不够卖带来的潜在收益损失(在电商中, 常见的由于备货不足, 销量非常好的商品由于无货, 导致相关的大流量的关键词检索排名下滑(或者在其他场景被推荐的排名大幅下滑), 甚至补货后, 排名也无法回到之前的高位, 额外的备货实际上需要有一定额度来应对可能出现的备货不足问题, 实际的一部分商品无法出售带来的损失相当于为搜索高排名的产品购买缺货的保险支出).
  • 补货的时间差带来的额外风险.
  • 补货需要考虑不同时期的订购商品的价格不一样(通常不同的订货数量也不一样的采购价格).
  • 资金是有限的, 但是投资确是不确定的, 需要考虑投资回报收益(也许单一模型调整的参数已是最优, 但是不是全局最优).
  • ....

四. 参考

大部分的处理方式都是一样的, 只是在数学模型参数上一些表述上的差异而已.

# operational research # matlab # math model # sympy # scipy # business # statistics # python
机器学习-梯度下降的简单理解 上一篇
Python关于数学的处理 下一篇
已运行:
浏览数: 次 | 访客数: 人
Powered by Kyouichirou